以企业Centos6.5Linux为案例来修复系统,步骤如下:
(1)远程备份本地其他重要数据,出现只读文件系统,需要先备份其他重要数据基于rsync|scp远程备份,其中/data为源目录,/data/backup/2017/为目标备份目录。
rsync -av /data/ root@192.168.111.188:/data/backup/2017/
(2) 可以重新挂载/系统,挂载命令如下,测试文件系统是否可以写入文件。
mount -o remount ,rw /
(3) 如果重新挂载/系统无法解决问题,则需重启服务器以CD/DVD光盘引导进入Linux Rescue修复模式。如图所示,光标选择Troubleshooting,按Enter键,然后选择Rescue a Centos system,按Enter。
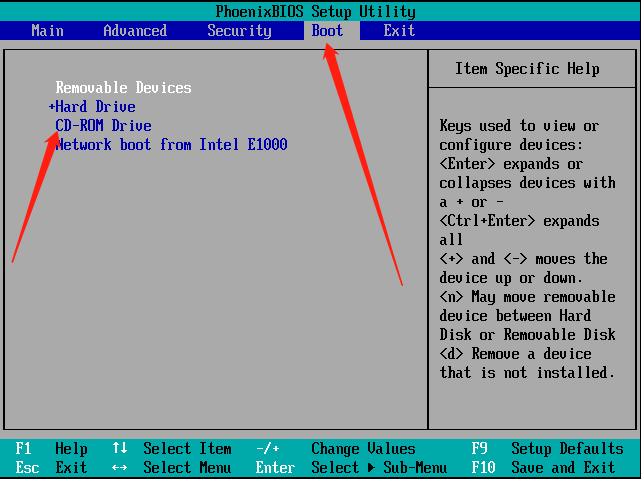
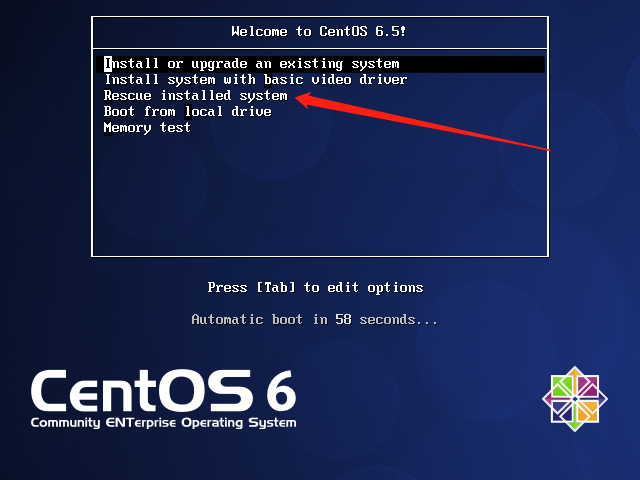
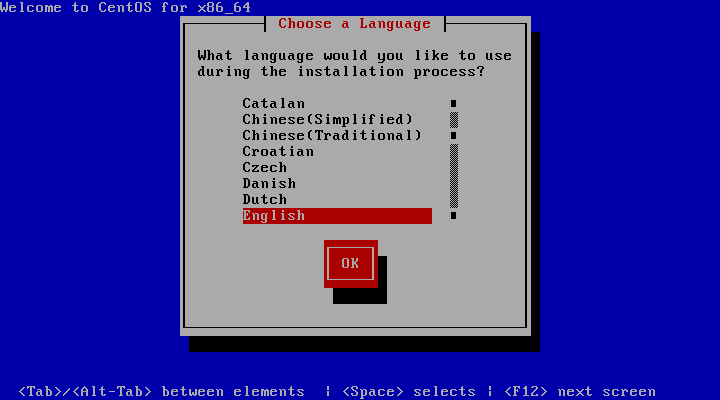
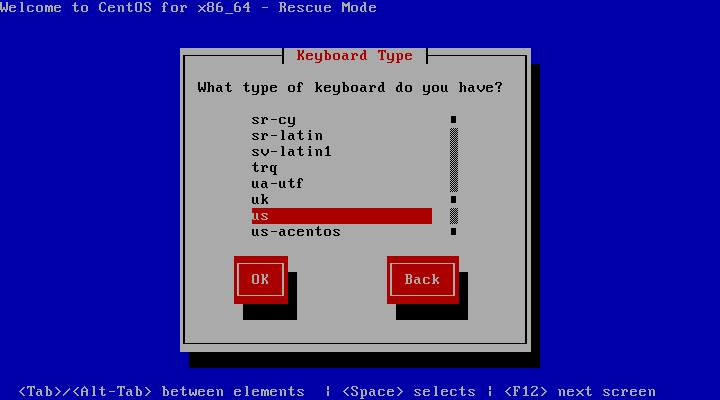
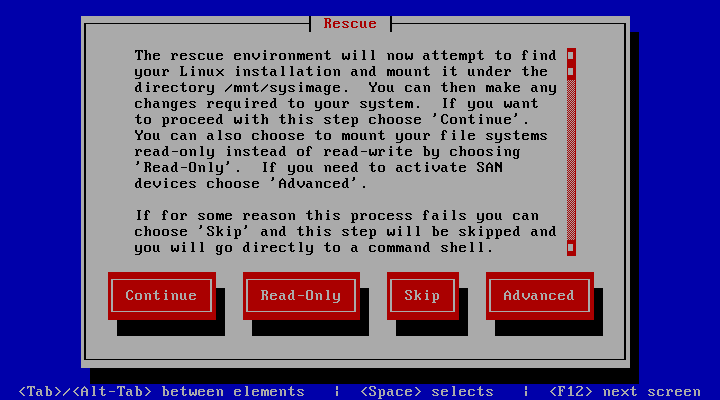
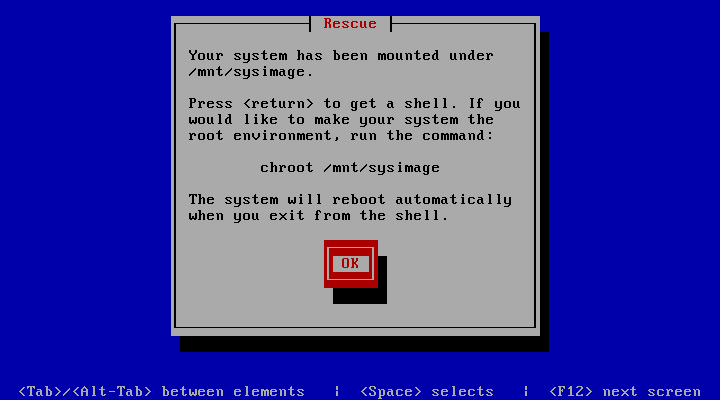
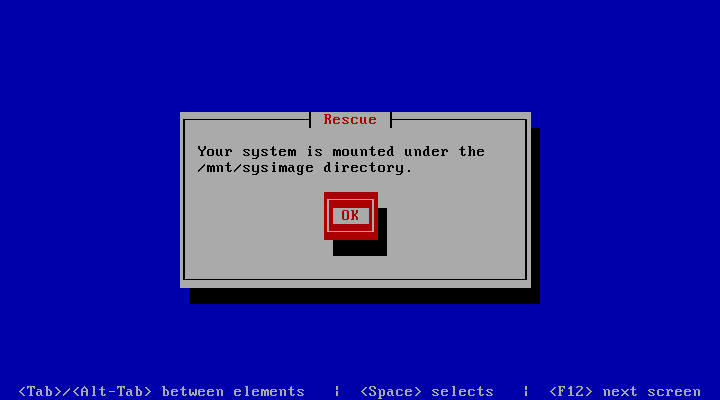
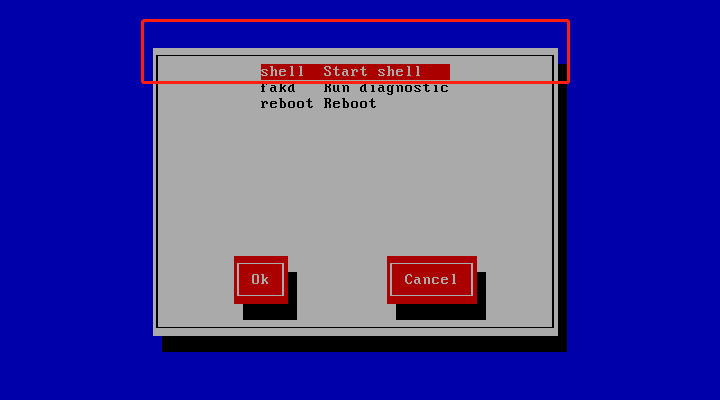
(4) 进入修复模式,执行如下命令,df -h 显示原来的文件系统,如图所示
df -h
chroot /mnt/sysimage 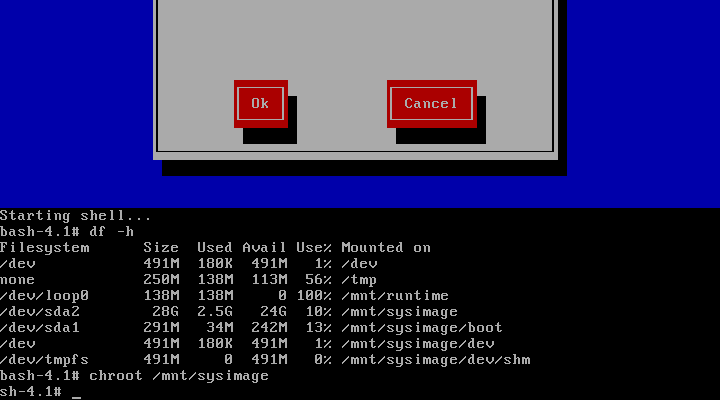
(5)对异常的分区进行检测并修复,根据文件系统的类型,执行命令如下:
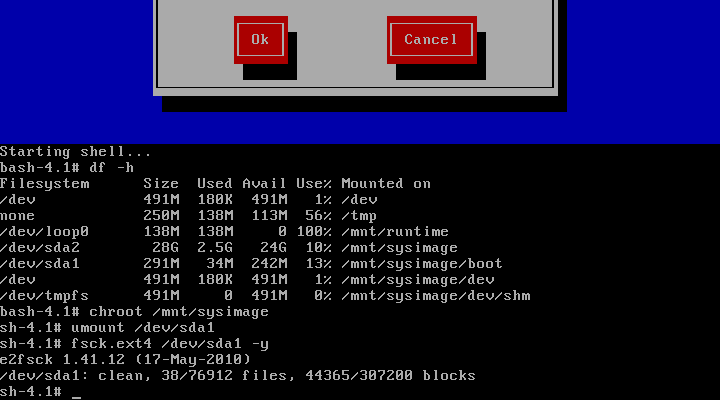
(6)修复完成之后,重启系统即可。
完成!
