网站建设及优化 赣icp电子商务企业网站建设实训报告
看了我Android低代码开发 - 让IDE帮你写代码这篇文章的小伙伴,大概都对Dora全家桶开发框架有基本的认识了吧。本篇文章将会讲解如何使用dora-studio-plugin快捷创建一个下拉刷新列表界面。
效果演示

这样直接通过图形界面的方式就创建好了下拉刷新上拉加载+空态界面+列表的基础代码,接下来开发起来就方便了。
依赖库
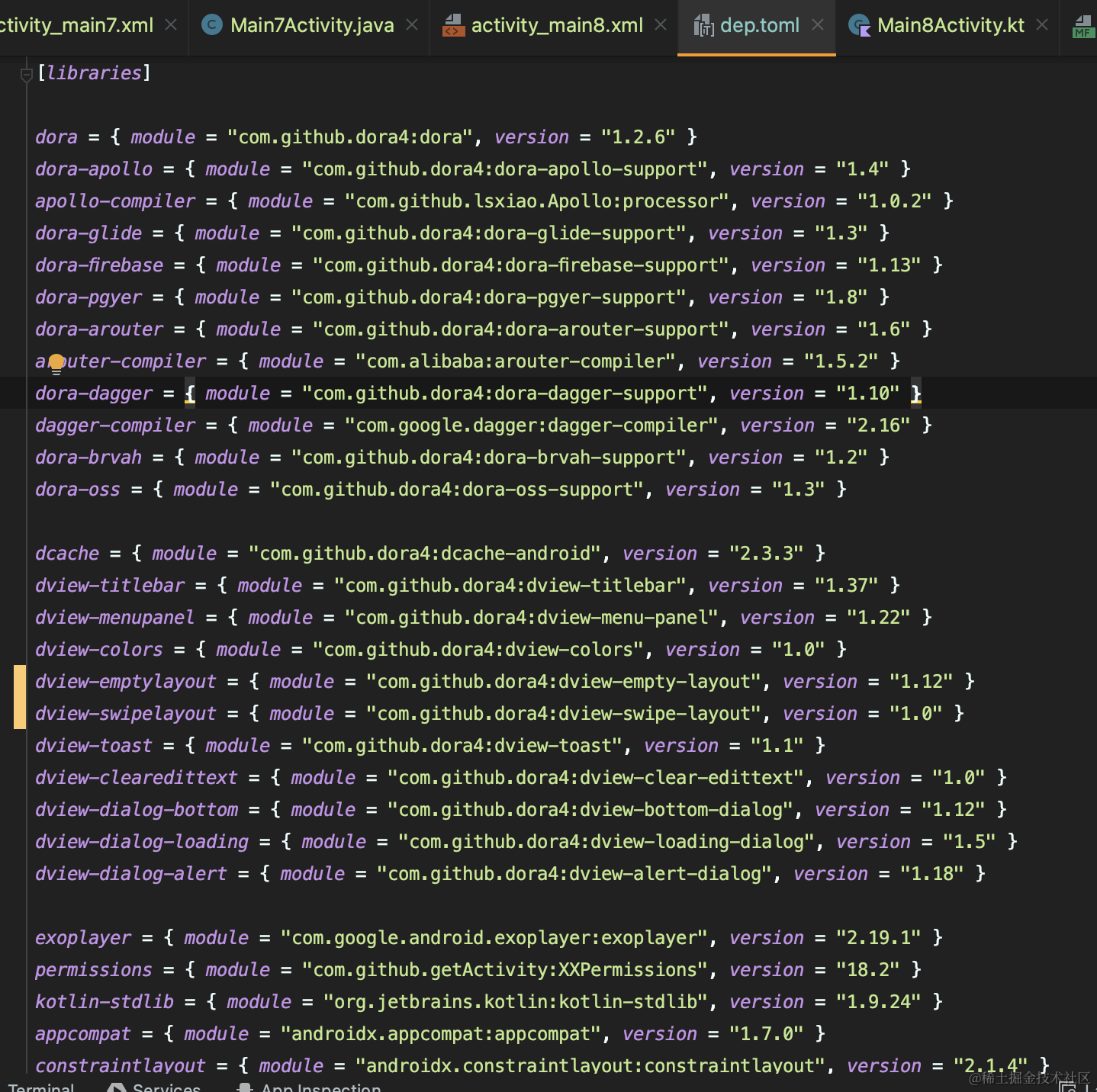
DoraTitleBar:建议用最新版本1.37
DoraEmptyLayout:必须用1.12版本
SwipeLayout和PullableRecyclerView:用1.0版本就好
IntelliJ IDEA插件1.4版本更新内容
生成布局文件的模板
/** Copyright (C) 2022 The Dora Open Source Project** Licensed under the Apache License, Version 2.0 (the "License");* you may not use this file except in compliance with the License.* You may obtain a copy of the License at** http://www.apache.org/licenses/LICENSE-2.0** Unless required by applicable law or agreed to in writing, software* distributed under the License is distributed on an "AS IS" BASIS,* WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.* See the License for the specific language governing permissions and* limitations under the License.*/package com.dorachat.templates.recipes.app_package.res.layoutfun swipeLayoutActivityXml(packageName: String,activityClass: String
) = """
<?xml version="1.0" encoding="utf-8"?>
<layout xmlns:android="http://schemas.android.com/apk/res/android"xmlns:app="http://schemas.android.com/apk/res-auto"xmlns:tools="http://schemas.android.com/tools"tools:context="${packageName}.${activityClass}"><data></data><LinearLayoutandroid:layout_width="match_parent"android:layout_height="match_parent"android:orientation="vertical"><dora.widget.DoraTitleBarandroid:id="@+id/titleBar"android:layout_width="match_parent"android:layout_height="50dp"app:dview_title="@string/app_name"android:background="@color/colorPrimary"/><dora.widget.DoraEmptyLayoutandroid:id="@+id/emptyLayout"android:layout_width="match_parent"android:layout_height="match_parent"><dora.widget.pull.SwipeLayoutandroid:id="@+id/swipeLayout"android:layout_width="match_parent"android:layout_height="match_parent"><include layout="@layout/layout_swipe_layout_header" /><dora.widget.pull.PullableRecyclerViewandroid:id="@+id/recyclerView"android:layout_width="match_parent"android:layout_height="match_parent"android:background="@color/colorPanelBg" /><include layout="@layout/layout_swipe_layout_footer" /></dora.widget.pull.SwipeLayout></dora.widget.DoraEmptyLayout></LinearLayout>
</layout>
"""
生成Java和Kotlin代码的模板
/** Copyright (C) 2022 The Dora Open Source Project** Licensed under the Apache License, Version 2.0 (the "License");* you may not use this file except in compliance with the License.* You may obtain a copy of the License at** http://www.apache.org/licenses/LICENSE-2.0** Unless required by applicable law or agreed to in writing, software* distributed under the License is distributed on an "AS IS" BASIS,* WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.* See the License for the specific language governing permissions and* limitations under the License.*/package com.dorachat.templates.recipes.app_package.srcfun swipeLayoutActivityKt(applicationPackage: String,packageName: String,activityClass: String,bindingName: String,layoutName: String
) = """
package ${packageName}import android.os.Bundleimport dora.BaseActivity
import dora.widget.pull.SwipeLayoutimport ${applicationPackage}.R
import ${applicationPackage}.databinding.${bindingName}class ${activityClass} : BaseActivity<${bindingName}>() {override fun getLayoutId(): Int {return R.layout.${layoutName}}override fun initData(savedInstanceState: Bundle?, binding: ${bindingName}) {TODO("Not yet implemented")// For Example:// binding.swipeLayout.setOnSwipeListener(object : SwipeLayout.OnSwipeListener {//// override fun onRefresh(swipeLayout: SwipeLayout) {// }//// override fun onLoadMore(swipeLayout: SwipeLayout) {// }// })}
}
"""fun swipeLayoutActivity(applicationPackage: String,packageName: String,activityClass: String,bindingName: String,layoutName: String
) = """
package ${packageName};import android.os.Bundle;
import androidx.annotation.Nullable;import dora.BaseActivity;
import dora.widget.pull.SwipeLayout;import ${applicationPackage}.R;
import ${applicationPackage}.databinding.${bindingName};public class ${activityClass} extends BaseActivity<${bindingName}> {@Overrideprotected int getLayoutId() {return R.layout.${layoutName};}@Overridepublic void initData(@Nullable Bundle savedInstanceState, ${bindingName} binding) {// TODO: Not yet implemented// For Example:// binding.swipeLayout.setOnSwipeListener(new SwipeLayout.OnSwipeListener() {//// @Override// public void onRefresh(SwipeLayout swipeLayout) {// }// // @Override// public void onLoadMore(SwipeLayout swipeLayout) {// }// });}
}
"""
DoraTemplateRecipe.kt新增生成代码的方法
fun RecipeExecutor.swipeLayoutActivityRecipe(moduleData: ModuleTemplateData,activityClass: String,activityTitle: String,layoutName: String,packageName: String
) {val (projectData, srcOut, resOut) = moduleDatagenerateManifest(moduleData = moduleData,activityClass = activityClass,packageName = packageName,isLauncher = false,hasNoActionBar = false,generateActivityTitle = false)if (projectData.language == Language.Kotlin) {save(swipeLayoutActivityKt(projectData.applicationPackage ?: packageName, packageName, activityClass,buildBindingName(layoutName), layoutName), srcOut.resolve("${activityClass}.${projectData.language.extension}"))}if (projectData.language == Language.Java) {save(swipeLayoutActivity(projectData.applicationPackage ?: packageName, packageName, activityClass,buildBindingName(layoutName), layoutName), srcOut.resolve("${activityClass}.${projectData.language.extension}"))}save(swipeLayoutActivityXml(packageName, activityClass), resOut.resolve("layout/${layoutName}.xml"))open(resOut.resolve("layout/${layoutName}.xml"))}
新增一个向导界面模板
/** Copyright (C) 2022 The Dora Open Source Project** Licensed under the Apache License, Version 2.0 (the "License");* you may not use this file except in compliance with the License.* You may obtain a copy of the License at** http://www.apache.org/licenses/LICENSE-2.0** Unless required by applicable law or agreed to in writing, software* distributed under the License is distributed on an "AS IS" BASIS,* WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.* See the License for the specific language governing permissions and* limitations under the License.*/package com.dorachat.templates.recipesimport com.android.tools.idea.wizard.template.*
import com.android.tools.idea.wizard.template.impl.activities.common.MIN_API
import java.io.Fileobject SwipeLayoutActivityTemplate : Template {override val category: Categoryget() = Category.Activityoverride val constraints: Collection<TemplateConstraint>get() = emptyList() // AndroidX, kotlinoverride val description: Stringget() = "创建一个dora.BaseActivity,来自https://github.com/dora4/dora"override val documentationUrl: String?get() = nulloverride val formFactor: FormFactorget() = FormFactor.Mobileoverride val minSdk: Intget() = MIN_APIoverride val name: Stringget() = "SwipeLayout DataBinding Activity"override val recipe: Recipeget() = {swipeLayoutActivityRecipe(it as ModuleTemplateData,activityClassInputParameter.value,activityTitleInputParameter.value,layoutNameInputParameter.value,packageName.value)}override val uiContexts: Collection<WizardUiContext>get() = listOf(WizardUiContext.ActivityGallery, WizardUiContext.MenuEntry, WizardUiContext.NewProject, WizardUiContext.NewModule)override val useGenericInstrumentedTests: Booleanget() = falseoverride val useGenericLocalTests: Booleanget() = falseoverride val widgets: Collection<Widget<*>>get() = listOf(TextFieldWidget(activityTitleInputParameter),TextFieldWidget(activityClassInputParameter),TextFieldWidget(layoutNameInputParameter),PackageNameWidget(packageName),LanguageWidget())override fun thumb(): Thumb {return Thumb { findResource(this.javaClass, File("template_activity.png")) }}val activityClassInputParameter = stringParameter {name = "Activity Name"default = "MainActivity"help = "The name of the activity class to create"constraints = listOf(Constraint.CLASS, Constraint.UNIQUE, Constraint.NONEMPTY)suggest = { layoutToActivity(layoutNameInputParameter.value) }}var layoutNameInputParameter: StringParameter = stringParameter {name = "Layout Name"default = "activity_main"help = "The name of the layout to create for the activity"constraints = listOf(Constraint.LAYOUT, Constraint.UNIQUE, Constraint.NONEMPTY)suggest = { activityToLayout(activityClassInputParameter.value) }}val activityTitleInputParameter = stringParameter {name = "Title"default = "Main"help = "The name of the activity. For launcher activities, the application title"visible = { false }constraints = listOf(Constraint.NONEMPTY)suggest = { buildClassNameWithoutSuffix(activityClassInputParameter.value, "Activity") }}val packageName = defaultPackageNameParameter
}
将向导界面模板添加到向导模板提供者
/** Copyright (C) 2022 The Dora Open Source Project** Licensed under the Apache License, Version 2.0 (the "License");* you may not use this file except in compliance with the License.* You may obtain a copy of the License at** http://www.apache.org/licenses/LICENSE-2.0** Unless required by applicable law or agreed to in writing, software* distributed under the License is distributed on an "AS IS" BASIS,* WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.* See the License for the specific language governing permissions and* limitations under the License.*/package com.dorachat.templates.recipesimport com.android.tools.idea.wizard.template.WizardTemplateProviderclass DoraTemplateWizardProvider: WizardTemplateProvider() {override fun getTemplates() = listOf(DataBindingActivityTemplate,DataBindingFragmentTemplate,MenuPanelActivityTemplate,SwipeLayoutActivityTemplate,MVVMActivityTemplate,MVVMFragmentTemplate)
}
更新版本日志
patchPluginXml {version.set("${project.version}")sinceBuild.set("213")untilBuild.set("223.*")changeNotes.set("""<h3>1.4</h3>新增对SwipeLayout的支持<br/><h3>1.3</h3>新增对MenuPanel的支持<br/><h3>1.2</h3>新增对BaseVMActivity和BaseVMFragment的支持<br/><h3>1.1</h3>initData()方法中增加databinding参数<br/><h3>1.0</h3>初始版本,能够创建Java和Kotlin版本的MVVM Activiy和MVVM Fragment<br/>""")
}
代码讲解
DoraEmptyLayout为什么可以识别SwipeLayout里面的RecyclerView?
open fun showContent() {runMain {if (contentView is RecyclerView) {if ((contentView as RecyclerView).adapter == null ||(contentView as RecyclerView).adapter!!.itemCount == 0) {showEmpty()return@runMain}}// 1.12开始支持遍历容器,确保一个EmptyLayout里面只能放一个RecyclerViewif (contentView is ViewGroup) {for (i in 0 until childCount) {val view = getChildAt(i)if (view is RecyclerView) {if (view.adapter == null ||view.adapter!!.itemCount == 0) {showEmpty()return@runMain}}}}val view = showStateView(STATE_CONTENT)this.content?.invoke(view)}
}
我们可以看到DoraEmptyLayout类从1.11升级到1.12版本的过程中,新增了以下代码来支持SwipeLayout。
if (contentView is ViewGroup) {for (i in 0 until childCount) {val view = getChildAt(i)if (view is RecyclerView) {if (view.adapter == null ||view.adapter!!.itemCount == 0) {showEmpty()return@runMain}}}
}
这样就不难理解了,如果遇到了刷新布局,如SwipeLayout,就再解析一层找RecyclerView。当然,一个DoraEmptyLayout里面只能放一个RecyclerView。
SwipeLayout是何方神圣?
- 支持暗色模式
- 支持英语、阿拉伯语、德语、西班牙语、法语、意大利语、日语、韩语、葡萄牙语、俄语、泰语、越南语、简体中文和繁体中文等世界10几个主流语种
- 支持自定义可拉动的内容布局
- 支持插件创建
- 与DoraEmptyLayout空态布局完美兼容(需要使用v1.12以上版本)
- 界面丝滑
通过PullableRecyclerView源码来看怎么自定义可拉动的内容布局
package dora.widget.pullimport android.content.Context
import android.util.AttributeSet
import androidx.recyclerview.widget.LinearLayoutManager
import androidx.recyclerview.widget.RecyclerView
import dora.widget.swipelayout.Rclass PullableRecyclerView @JvmOverloads constructor(context: Context, attrs: AttributeSet? = null,defStyle: Int = 0): RecyclerView(context, attrs, defStyle), Pullable {private var canPullDown = trueprivate var canPullUp = trueinit {val a = context.obtainStyledAttributes(attrs, R.styleable.PullableRecyclerView, defStyle, 0)canPullDown = a.getBoolean(R.styleable.PullableRecyclerView_dview_canPullDown, canPullDown)canPullUp = a.getBoolean(R.styleable.PullableRecyclerView_dview_canPullUp, canPullUp)a.recycle()}fun setCanPullDown(canPullDown: Boolean) {this.canPullDown = canPullDown}fun setCanPullUp(canPullUp: Boolean) {this.canPullUp = canPullUp}override fun canPullDown(): Boolean {return if (canPullDown) {val layoutManager = layoutManager as LinearLayoutManager?val adapter = adapterif (adapter != null) {return if (adapter.itemCount == 0) {false} else layoutManager!!.findFirstVisibleItemPosition() == 0&& getChildAt(0).top >= 0}false} else {false}}override fun canPullUp(): Boolean {if (canPullUp) {val layoutManager = layoutManager as LinearLayoutManagerif (adapter != null && adapter?.itemCount!! == 0) {return false} else if (layoutManager.findLastVisibleItemPosition() == ((adapter as Adapter).itemCount - 1)) {// 滑到底部了if (getChildAt(layoutManager.findLastVisibleItemPosition() - layoutManager.findFirstVisibleItemPosition()) != null&& getChildAt(layoutManager.findLastVisibleItemPosition()- layoutManager.findFirstVisibleItemPosition()).bottom <= measuredHeight) {return true}}return false} else {return false}}
}
它实现了一个顶层接口Pullable,通过canPullDown()和canPullUp()两个方法来在运行时动态判断可不可以下拉刷新和上拉加载。
private var canPullDown = true
private var canPullUp = true
里面提供了两个属性,表示是否有下拉和上拉能力,如果设置为false,则无论条件达成与否都不能进行刷新和加载。
<dora.widget.pull.PullableRecyclerViewandroid:id="@+id/recyclerView"android:layout_width="match_parent"android:layout_height="match_parent"android:background="@color/colorPanelBg"app:dview_canPullDown="true"app:dview_canPullUp="false"/>
可以通过属性设置这两个变量,比如不需要上拉加载就把上拉的设置为false,app:dview_canPullUp=“false”。
设置完成刷新和加载的监听
binding.swipeLayout.setOnSwipeListener(new SwipeLayout.OnSwipeListener() {@Overridepublic void onRefresh(SwipeLayout swipeLayout) {}@Overridepublic void onLoadMore(SwipeLayout swipeLayout) {}
});
通过调用swipeLayout的refreshFinish(state)和loadMoreFinish(state)来结束刷新和加载状态。
const val SUCCEED = 0
const val FAIL = 1
有成功和失败两种状态可以设置。所以,你在onRefresh()或onLoadMore()的最后一行调用刷新状态即可。
源码链接
下拉刷新:https://github.com/dora4/dview-swipe-layout
空态布局:https://github.com/dora4/dview-empty-layout
代码生成插件:https://github.com/dora4/dora-studio-plugin
