长沙优秀网站建设软件技术就业前景怎么样
git官网:https://git-scm.com
git使用手册:https://git-scm.com/book/zh/v2
一、Git 是什么?
1、版本控制
版本控制是一种记录一个或若干文件内容变化,以便将来查阅特定版本修订情况的系统。我们经常是用的是保存软件源代码的文件作版本控制,但实际上,任何类型的文件都可以进行版本控制。
有了它你就可以将选定的文件回溯到之前的状态,甚至将整个项目都回退到过去某个时间点的状态,你可以比较文件的变化细节,查出最后是谁修改了哪个地方,从而找出导致怪异问题出现的原因,又是谁在何时报告了某个功能缺陷等等。 使用版本控制系统通常还意味着,就算你乱来一气把整个项目中的文件改的改删的删,你也照样可以轻松恢复到原先的样子。 但额外增加的工作量却微乎其微。
有三种类型:本地版本控制系统、 集中化的版本控制系统、 分布式版本控制系统。(详解)
2、是什么
git概念和特点
3、命令行
Git 有多种使用方式。 你可以使用原生的命令行模式,也可以使用 GUI 模式,这些 GUI 软件也能提供多种功能。
一定要学会命令行
只有在命令行模式下你才能执行 Git 的 所有 命令,而大多数的 GUI 软件只实现了 Git 所有功能的一个子集以降低操作难度。 如果你学会了在命令行下如何操作,那么你在操作 GUI 软件时应该也不会遇到什么困难,但是,反之则不成立。
假如是 macOS 用户要懂得使用终端(Terminal);假如是 Windows 用户要懂得如何使用命令窗口(Command Prompt)或 PowerShell。
二、安装Git和升级
1、Windows安装
主要讲Windows环境下的安装。
进入官网,win系统直接点击这里,就会开始下载安装包。

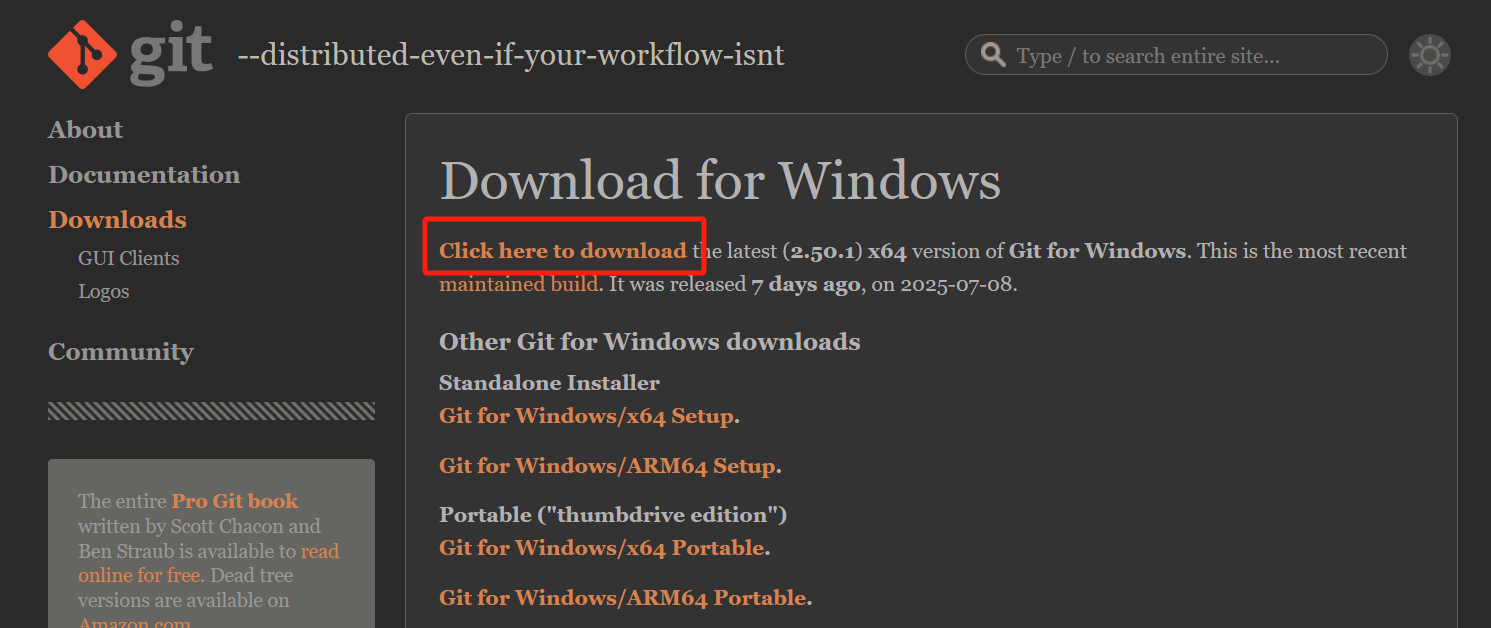
安装包打开,一直点击next就可以,需要修改安装地址的注意在安装地址那页修改一下。
安装成功后桌面右键会显示Git GUI Here和Git Bash Here。Git Bash Here打开的是当前目录下的命令行窗口。
2、其他环境
git安装
3、win环境更新git版本
桌面右键打开终端
git --version //查看版本号
git update-git-for-windows三、初次运行 Git 前的配置
1、git config
Git 自带一个 git config 的工具来帮助设置控制 Git 外观和行为的配置变量。
这些变量存储在三个不同的位置:
/etc/gitconfig文件: 包含系统上每一个用户及他们仓库的通用配置。 如果在执行git config时带上--system选项,那么它就会读写该文件中的配置变量。 (由于它是系统配置文件,因此你需要管理员或超级用户权限来修改它。)
~/.gitconfig或~/.config/git/config文件:只针对当前用户。 你可以传递--global选项让 Git 读写此文件,这会对你系统上 所有 的仓库生效。当前使用仓库的 Git 目录中的
config文件(即.git/config):针对该仓库。 你可以传递--local选项让 Git 强制读写此文件,虽然默认情况下用的就是它。 (当然,你需要进入某个 Git 仓库中才能让该选项生效。)每一个级别会覆盖上一级别的配置,所以
.git/config的配置变量会覆盖/etc/gitconfig中的配置变量。
1-1 配置name和email
安装完 Git 之后,要做的第一件事就是设置你的用户名和邮件地址。 这一点很重要,因为每一个 Git 提交都会使用这些信息,它们会写入到你的每一次提交中,不可更改:
$ git config --global user.name '名称'
$ git config --global user.email '邮箱'1-2 检查配置
$ git config --list
$ git config -l这两个命令是一样的,回车后会显示config 内容,如果出现还在文件中的情况,可以尝试用vim中的:wq命令退出。
2、Windows添加环境变量
在 Windows 系统中,Git 会查找
$HOME目录下(一般情况下是C:\Users\$USER)的.gitconfig文件。 Git 同样也会寻找/etc/gitconfig文件,但只限于 MSys 的根目录下,即安装 Git 时所选的目标位置。 如果你在 Windows 上使用 Git 2.x 以后的版本,那么还有一个系统级的配置文件,Windows XP 上在C:\Documents and Settings\All Users\Application Data\Git\config,Windows Vista 及其以后的版本在C:\ProgramData\Git\config。此文件只能以管理员权限通过git config -f <file>来修改。
这里的环境变量就是我们常用的那个。
找到path,在里面添加上git的bin目录和cmd目录
3、文本编辑器
既然用户信息已经设置完毕,你可以配置默认文本编辑器了,当 Git 需要你输入信息时会调用它。 如果未配置,Git 会使用操作系统默认的文本编辑器。
如果你想使用不同的文本编辑器,例如 Emacs,可以这样做:
$ git config --global core.editor emacs在 Windows 系统上,如果你想要使用别的文本编辑器,那么必须指定可执行文件的完整路径。 它可能随你的编辑器的打包方式而不同。
对于 Notepad++,一个流行的代码编辑器来说,你可能想要使用 32 位的版本, 因为在本书编写时 64 位的版本尚不支持所有的插件。 如果你在使用 32 位的 Windows 系统,或在 64 位系统上使用 64 位的编辑器,那么你需要输入如下命令:
$ git config --global core.editor "'C:/Program Files/Notepad++/notepad++.exe' -multiInst -notabbar -nosession -noPlugin"四、help命令
若你使用 Git 时需要获取帮助,有三种等价的方法可以找到 Git 命令的综合手册:
$ git help <verb>
$ git <verb> --help
$ man git-<verb>例如 :
$ git help config
$ git add -h