高校工会网站建设如何给公司建立网站
前言
前段时间完成了C#经典十大排序算法(完结)然后有很多小伙伴问想要系统化的学习数据结构和算法,不知道该怎么入门,有无好的教程推荐的。今天给大家推荐一个支持C#的开源免费、新手友好的数据结构与算法入门教程:Hello算法。
Hello算法介绍
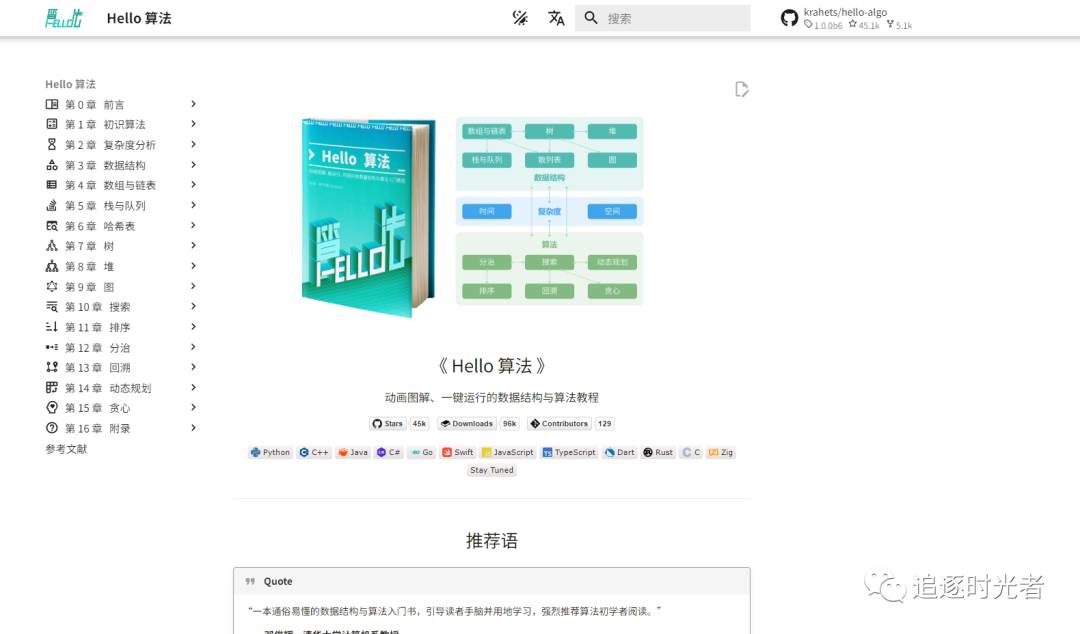
Hello算法一个开源免费、新手友好的数据结构与算法入门教程。
-
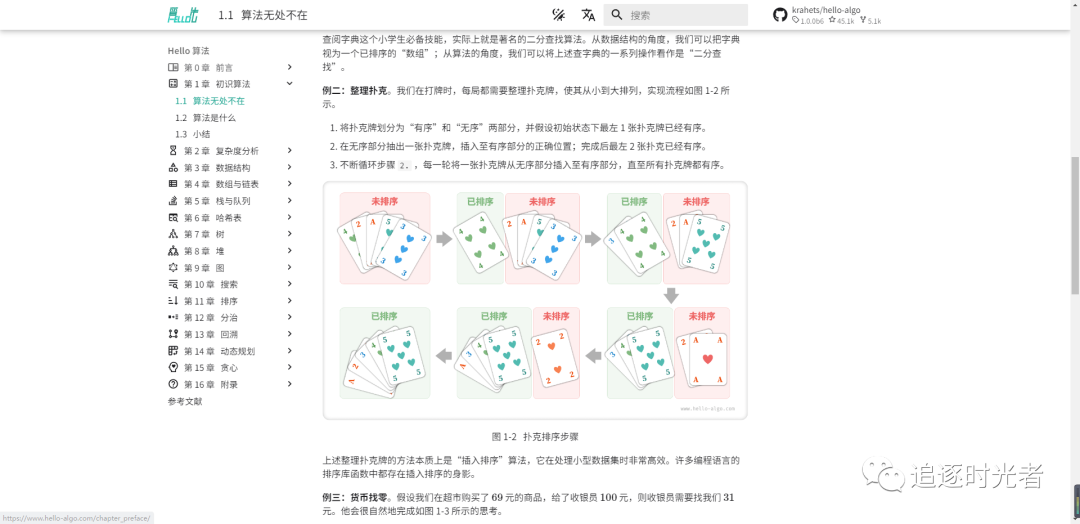
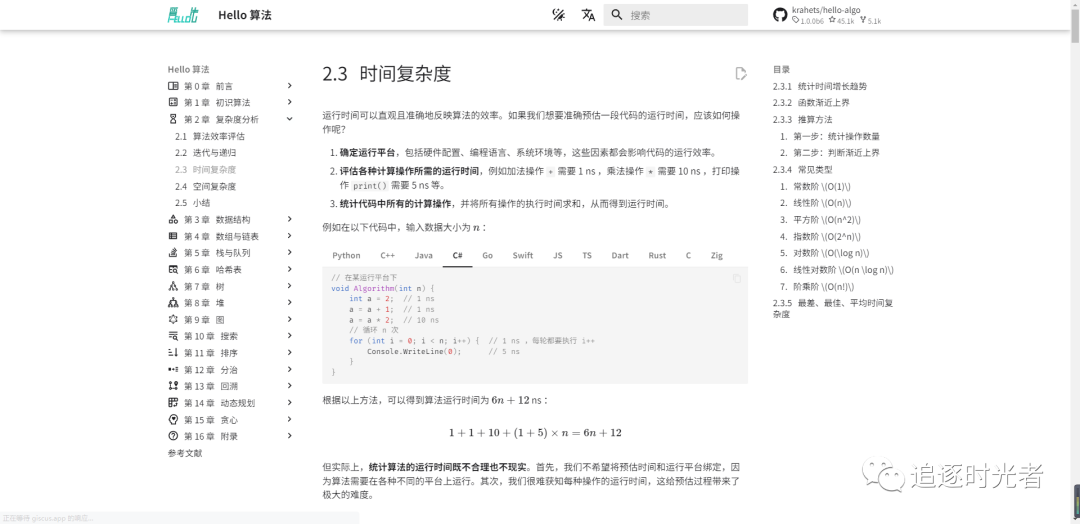
全书采用动画图解,内容清晰易懂、学习曲线平滑,引导初学者探索数据结构与算法的知识地图。
-
源代码可一键运行,帮助读者在练习中提升编程技能,了解算法工作原理和数据结构底层实现。
-
支持 Java, C++, Python, Go, JS, TS, C#, Swift, Rust, Dart, Zig 等语言。
内容结构

项目下载并使用Visual Studio2022打开
-
GitHub开源地址:https://github.com/krahets/hello-algo
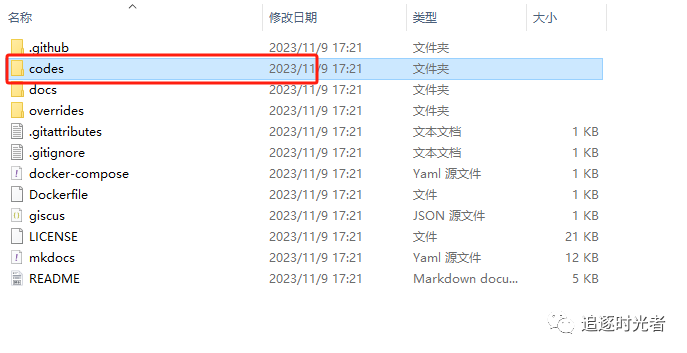
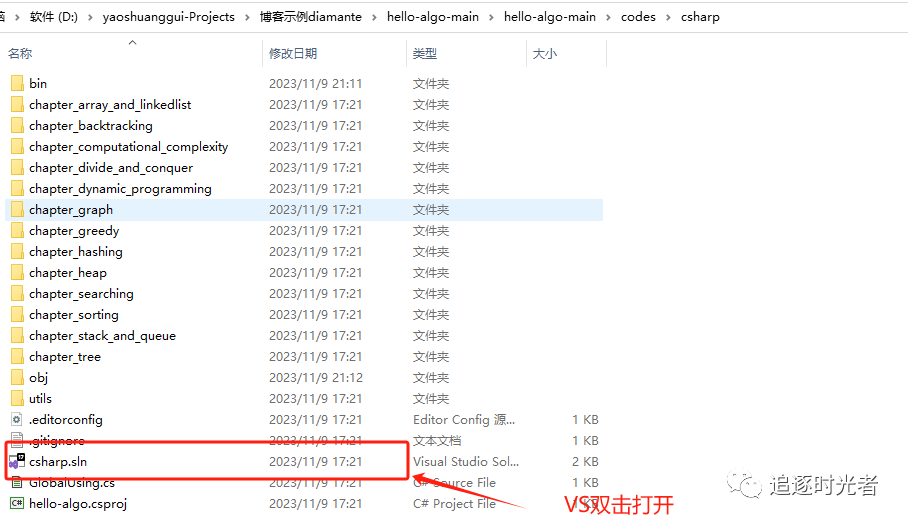
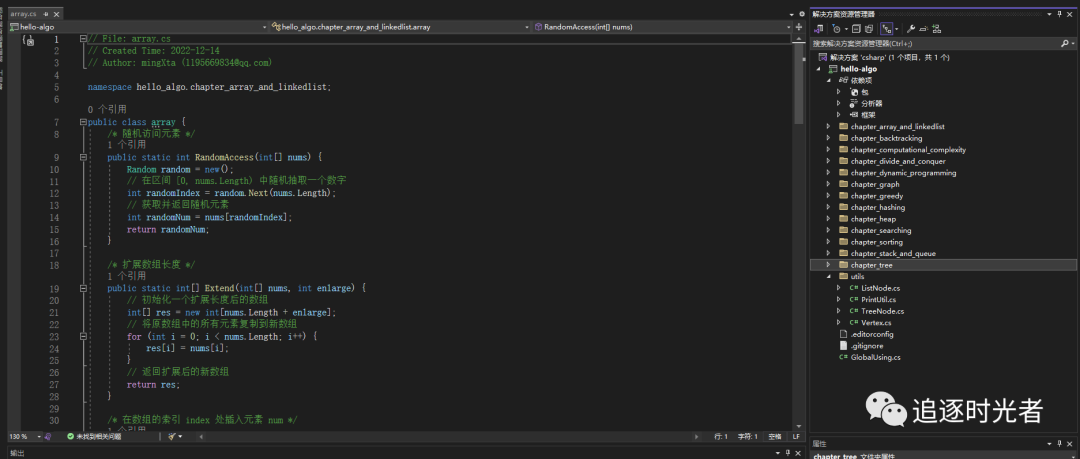
运行C#相关数据结构与算法示例
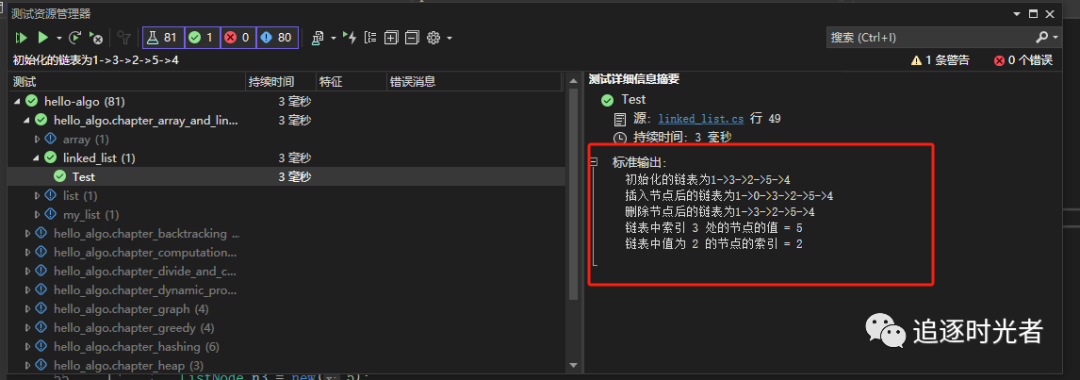
链表
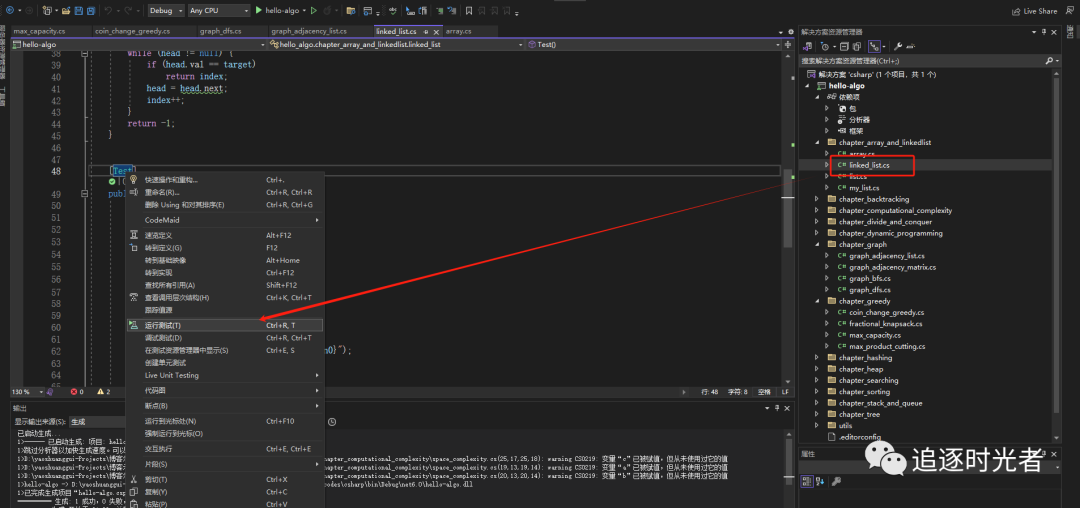
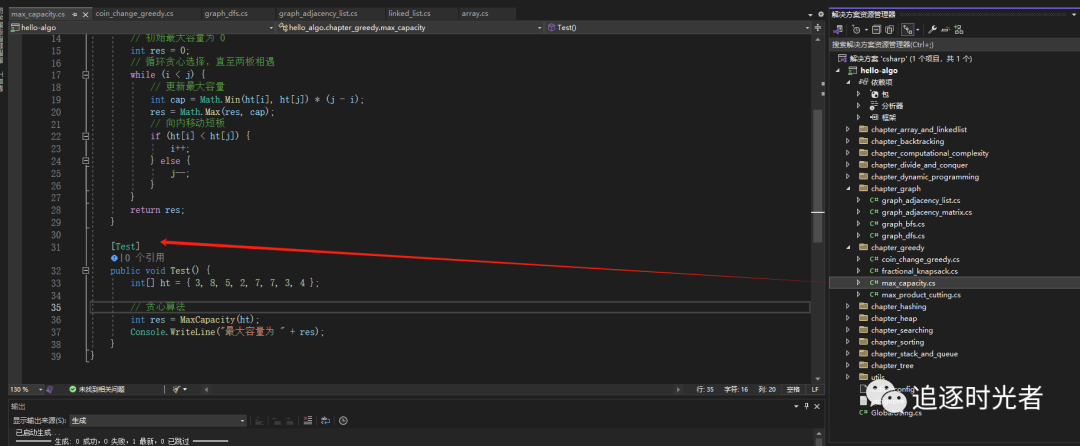
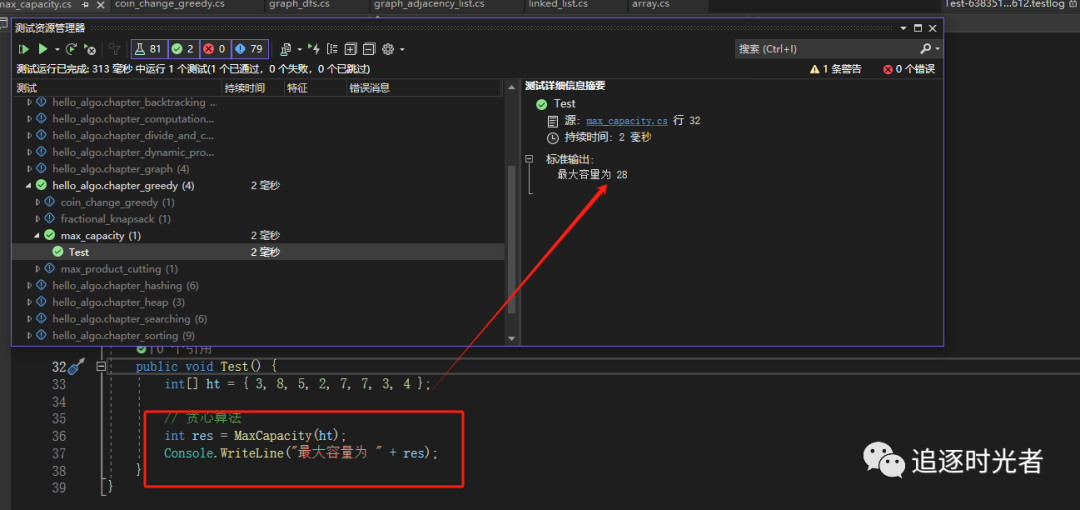
贪心算法
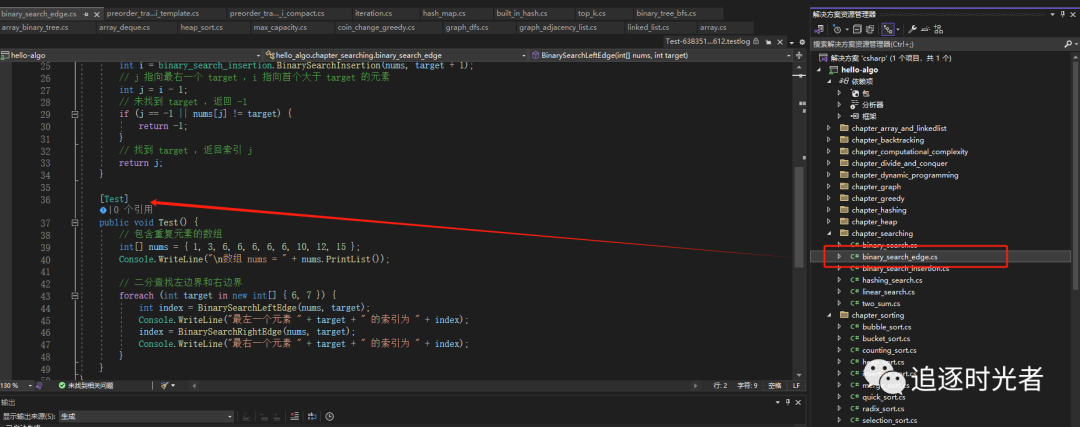
二分查找算法
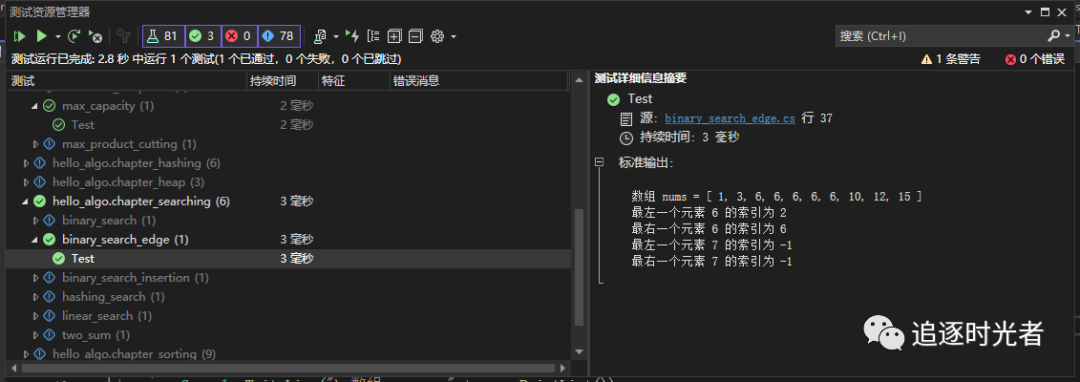
在线预览
-
在线预览地址:https://www.hello-algo.com/


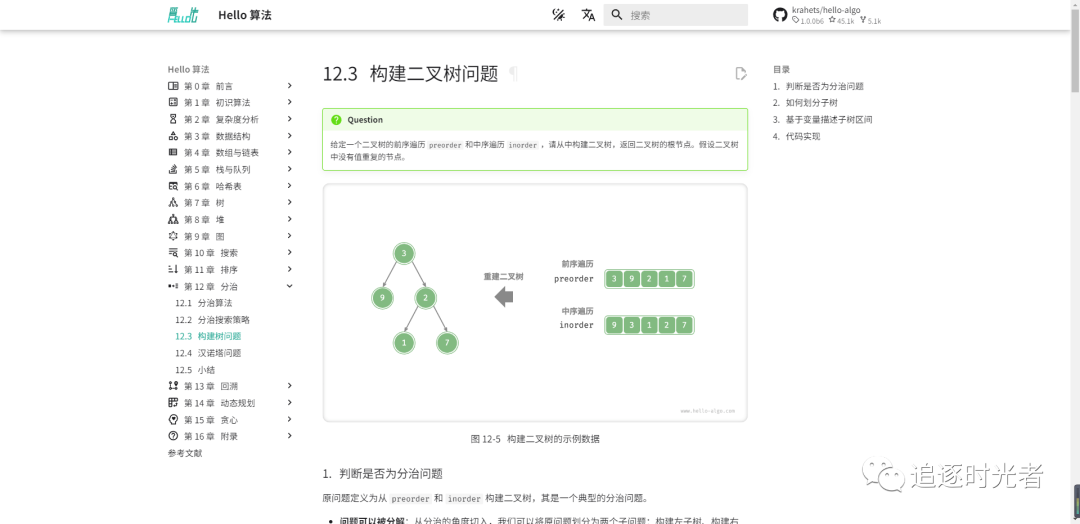
获取更多逻辑算法学习资料
关注公众号
追逐时光者回复关键字:算法。
项目源码地址
更多项目实用功能和特性欢迎前往项目开源地址查看👀,别忘了给项目一个Star支持💖。
Github开源地址:https://github.com/krahets/hello-algo
直接访问地址:https://www.hello-algo.com/
优秀项目和框架精选
该项目已收录到C#/.NET/.NET Core优秀项目和框架精选中,关注优秀项目和框架精选能让你及时了解C#、.NET和.NET Core领域的最新动态和最佳实践,提高开发工作效率和质量。坑已挖,欢迎大家踊跃提交PR推荐或自荐(让优秀的项目和框架不被埋没🤞)。
https://github.com/YSGStudyHards/DotNetGuide/blob/main/docs/DotNet/DotNetProjectPicks.md
