玉溪市住房和城乡建设局网站商标交易网
ESP32S3入手体验测试
- 🔖所入手的型号是
YD-ESP32-S3 N16R8,该款和乐鑫官方推出的ESP32-S3-DevKitC-1配置差不多。
- 🎈乐鑫官方介绍:ESP32-S3-DevKitC-1 v1.1
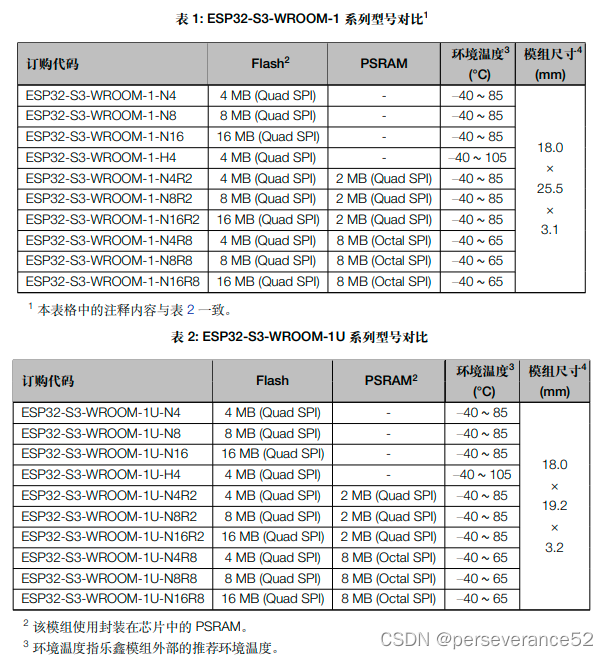
- 🔰两者采用的模组:ESP32-S3-WROOM-1 和ESP32-S3-WROOM-1U模组对比:
- 🍁
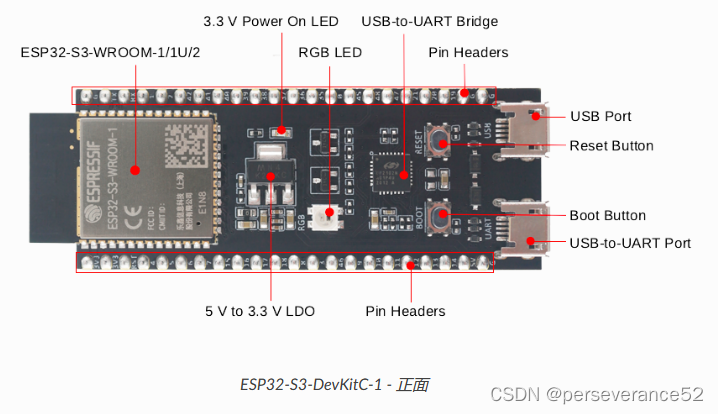
YD-ESP32-S3和ESP32-S3-DevKitC-1硬件基本信息:

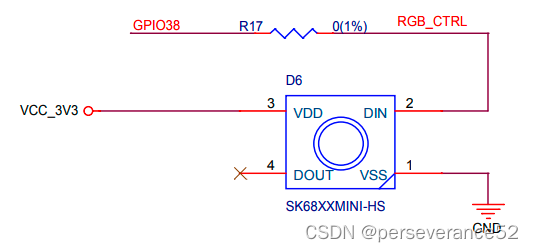
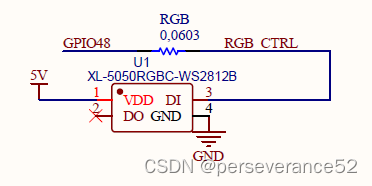
- 🛠核心模组配置都是可选。两款开发板从原理图上看,板载WS2812b灯珠所连接的芯片GPIO引脚不相同。YD-ESP32-S3板载WS2812B引脚:GPIO 48 ESP32-S3-DevKitC-1板载WS2812B引脚:GPIO38
📑Micropython测试
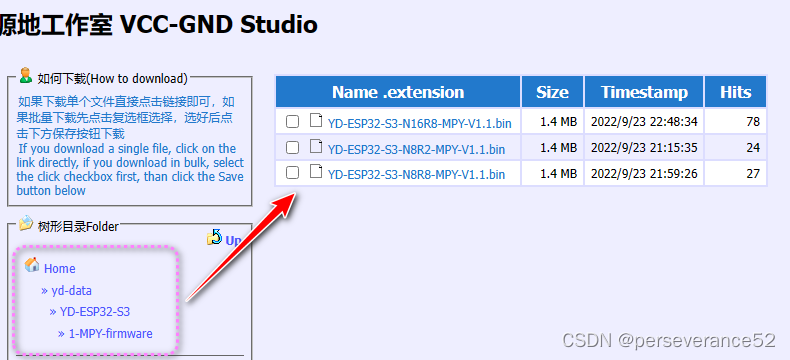
- 📋YD ESP32S3 Micropython固件下载地址可以去官方也可以去YD官网下载,根据个人所使用的型号选择对应的固件。
-
📍YD固件提供地址:
http://vcc-gnd.com:8080/yd-data/YD-ESP32-S3/1-MPY-firmware/
-
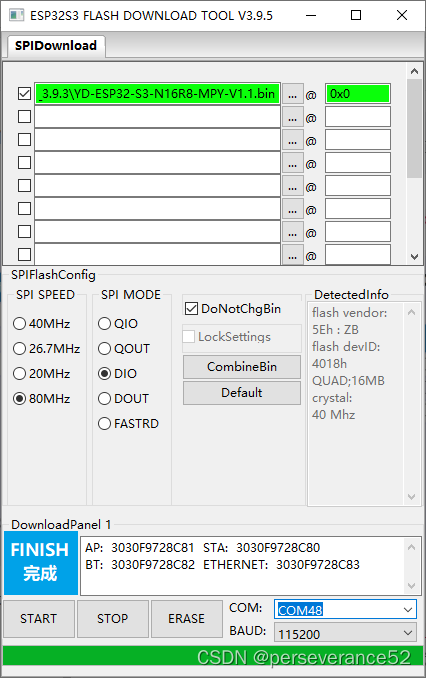
🔨固件烧录采用乐鑫官方的烧录工具
flash_download_tool_3.9.5进行烧录,烧录地址:0x0,切记不要使用Thonny软件进行烧录,它默认烧录地址是0x1000。
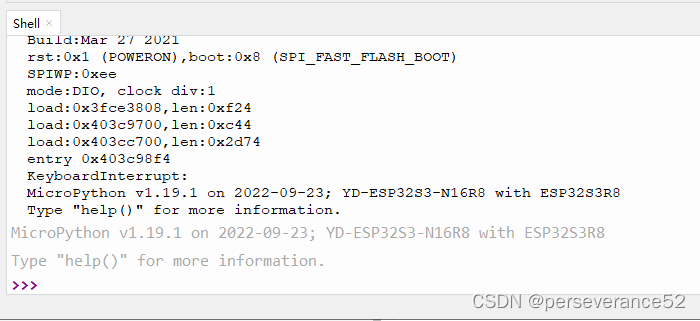
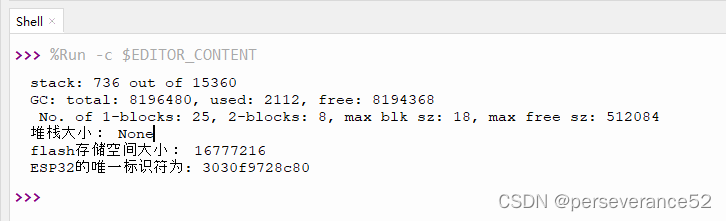
固件烧录完成后,通过Thonny软件,重启设备可以查看到打印的硬件配置信息。
-
🌿YD提供的micropython测试代码点亮板子WS2812b灯:
http://vcc-gnd.com:8080/yd-data/YD-ESP32-S3/4-MPY-Test-Python-DEMO/
from machine import Pin
from neopixel import NeoPixel
import timepin = Pin(48, Pin.OUT)
np = NeoPixel(pin, 1) # 一颗灯珠
np[0] = (10,0,0)
np.write()
r, g, b = np[0]
def handle_interrupt(Pin):np[0] = (0, 0, 0)np.write()time.sleep_ms(150)np[0] = (0, 0, 10)np.write()time.sleep_ms(150)np[0] = (0, 0, 10)np.write()time.sleep_ms(150)np[0] = (0, 0, 0)np.write()time.sleep_ms(150)np[0] = (0, 10, 0)np.write()time.sleep_ms(150)print("test-usr key")
p0 = Pin(0)
p0.init(p0.IN, p0.PULL_UP)
p0.irq(trigger=p0.IRQ_FALLING, handler=handle_interrupt)
- 🌿通过micropython查看硬件配置信息:
import machine
import esp
import micropython
# 打印堆栈大小
# print("堆栈大小:", esp.get_free_heap())
print("堆栈大小:", micropython.mem_info())
# 打印flash存储空间大小
print("flash存储空间大小:", esp.flash_size())
# 读取ESP32的唯一标识符
unique_id = machine.unique_id()# 将字节数组转换为可打印的字符串
unique_id_str = ''.join(['{:02x}'.format(byte) for byte in unique_id])print("ESP32的唯一标识符为:", unique_id_str)
- ⚡测试时需要注意:GPIO48引脚默认是没有直接联通到GPIO48引脚的,需要自行焊接一起。

- 🌿原图地址:
http://vcc-gnd.com:8080/yd-data/YD-ESP32-S3/5-public-YD-ESP32-S3-Hardware%20info/YD-ESP32-S3.PNG
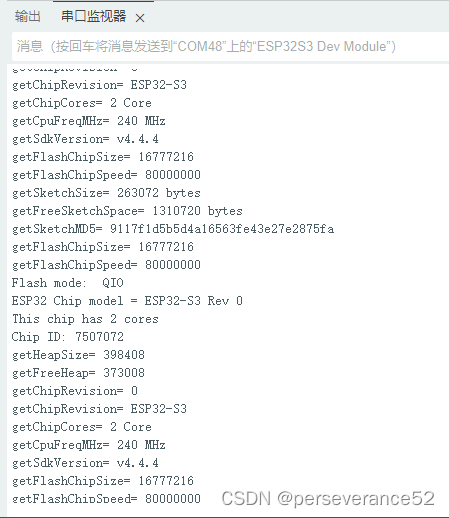
Arduino硬件配置信息打印
-
🔧型号以及参数配置:

-
📝打印硬件配置信息代码:
/*
使用源地ESP32S3开发板:YD-ESP32-S3
兼容乐鑫官方的ESP32-S3-DevKitC-1
:YD-ESP32-S3板载WS2812B引脚:GPIO 48
ESP32-S3-DevKitC-1板载WS2812B引脚:GPIO38*/uint32_t chipId = 0;
void setup() {// put your setup code here, to run once:Serial.begin(115200);
}void loop() {for(int i=0; i<17; i=i+8) {chipId |= ((ESP.getEfuseMac() >> (40 - i)) & 0xff) << i;}Serial.printf("ESP32 Chip model = %s Rev %d\n", ESP.getChipModel(), ESP.getChipRevision());//ESP32-S3 Rev 0Serial.printf("This chip has %d cores\n", ESP.getChipCores());//2Serial.print("Chip ID: "); Serial.println(chipId);// 7507072delay(10);
Serial.printf("getHeapSize= %d \n",ESP.getHeapSize());//399848
delay(10);
Serial.printf("getFreeHeap= %d \n",ESP.getFreeHeap());// 374924 delay(10);Serial.printf("getChipRevision= %d \n",ESP.getChipRevision()); // 0delay(10);Serial.printf("getChipRevision= %s \n",ESP.getChipModel()); //ESP32-S3 delay(10);Serial.printf("getChipCores= %d Core\n",ESP.getChipCores()); // 2 Coredelay(10);Serial.printf("getCpuFreqMHz= %d MHz\n",ESP.getCpuFreqMHz()); //240 MHz
delay(10);
Serial.printf("getSdkVersion= %s \n",ESP.getSdkVersion()); //v4.4.4
Serial.printf("getFlashChipSize= %d \n",ESP.getFlashChipSize());//16777216Serial.printf("getFlashChipSpeed= %d \n",ESP.getFlashChipSpeed());//80000000 Serial.printf("getSketchSize= %d bytes\n",ESP.getSketchSize()); //250128delay(10);Serial.printf("getFreeSketchSpace= %d bytes\n",ESP.getFreeSketchSpace()); //13631488 bytesdelay(10);Serial.printf("getSketchMD5= %s \n",ESP.getSketchMD5().c_str());//9117f1d5b5d4a16563fe43e27e2875fa delay(10);uint32_t flash_Size = ESP.getFlashChipSize(); Serial.printf("getFlashChipSize= %d \n",flash_Size); //16777216
delay(10);Serial.printf("getFlashChipSpeed= %d \n",ESP.getFlashChipSpeed()); //80000000delay(10);FlashMode_t flash_Mode = ESP.getFlashChipMode();Serial.printf("Flash mode: %s\n", (flash_Mode == FM_QIO ? "QIO" : flash_Mode == FM_QOUT ? "QOUT" : flash_Mode == FM_DIO ? "DIO" : flash_Mode == FM_DOUT ? "DOUT" : "UNKNOWN"));//QIOdelay(1000);
}