做网站v1认证是什么意思猪八戒网网站设计
最近调研流程引擎相关知识,BPMN规范和流程引擎相关知识无法避开,以及市面上比较多的流程引擎产品。
BPMN2.0
基本形状


- 流对象(Flow Objects),流对象是定义业务流程的主要图形元素。它进一步细分为三个类别,分别是事件(Events)、活动(Activities)和网关(Gateways);
- 数据(Data),它分为四个类别:数据对象(Data Object)、数据输入(Data Inputs)、数据输出(Data Outputs)和数据存储(Data Stores);
- 连接对象(Connection Ojbects),用来把各个流对象或流对象与其他信息连接起来,它分为四种类别:顺序流(Sequence Flows)、消息流(Message Flows)、关联(Associations)和数据关联(Data Associations);
- 泳道(Swimlanes),用来区分不同部门或者不同参与者的功能和职责。Swimlanes包含两种类别:池(Pool)和道(Lane);
- 人工交付物(Artifacts),它用以给流程附加一些额外的信息,它分为两种类别:组(Group)和附注(Text Annotation)。
BPMN2.0 规范
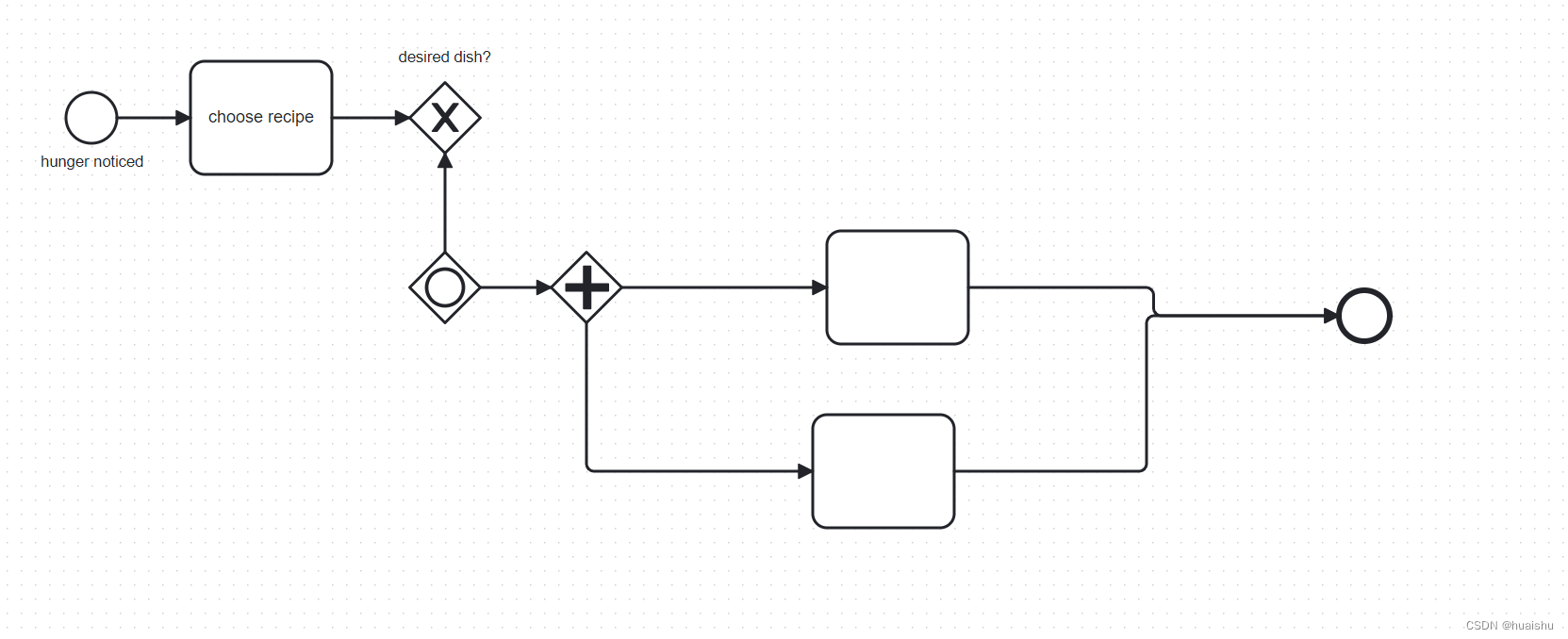
<?xml version="1.0" encoding="UTF-8"?>
<definitions xmlns="http://www.omg.org/spec/BPMN/20100524/MODEL" xmlns:bpmndi="http://www.omg.org/spec/BPMN/20100524/DI" xmlns:omgdi="http://www.omg.org/spec/DD/20100524/DI" xmlns:omgdc="http://www.omg.org/spec/DD/20100524/DC" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance" id="sid-38422fae-e03e-43a3-bef4-bd33b32041b2" targetNamespace="http://bpmn.io/bpmn" exporter="bpmn-js (https://demo.bpmn.io)" exporterVersion="15.1.3"><process id="Process_1" isExecutable="false"><startEvent id="StartEvent_1y45yut" name="hunger noticed"><outgoing>SequenceFlow_0h21x7r</outgoing></startEvent><task id="Task_1hcentk" name="choose recipe"><incoming>SequenceFlow_0h21x7r</incoming><outgoing>SequenceFlow_0wnb4ke</outgoing></task><sequenceFlow id="SequenceFlow_0h21x7r" sourceRef="StartEvent_1y45yut" targetRef="Task_1hcentk" /><exclusiveGateway id="ExclusiveGateway_15hu1pt" name="desired dish?"><incoming>SequenceFlow_0wnb4ke</incoming><incoming>Flow_0xtm5qb</incoming></exclusiveGateway><sequenceFlow id="SequenceFlow_0wnb4ke" sourceRef="Task_1hcentk" targetRef="ExclusiveGateway_15hu1pt" /><inclusiveGateway id="Gateway_09q2xe7"><outgoing>Flow_0xtm5qb</outgoing><outgoing>Flow_0xv9yxo</outgoing></inclusiveGateway><sequenceFlow id="Flow_0xtm5qb" sourceRef="Gateway_09q2xe7" targetRef="ExclusiveGateway_15hu1pt" /><sequenceFlow id="Flow_0xv9yxo" sourceRef="Gateway_09q2xe7" targetRef="Gateway_10k824i" /><task id="Activity_1yfhd3x"><incoming>Flow_1wboruz</incoming><outgoing>Flow_1flrhu1</outgoing></task><sequenceFlow id="Flow_1wboruz" sourceRef="Gateway_10k824i" targetRef="Activity_1yfhd3x" /><endEvent id="Event_1hdhify"><incoming>Flow_1flrhu1</incoming><incoming>Flow_0ekoeag</incoming></endEvent><sequenceFlow id="Flow_1flrhu1" sourceRef="Activity_1yfhd3x" targetRef="Event_1hdhify" /><task id="Activity_17jbx0j"><incoming>Flow_05xtbpr</incoming><outgoing>Flow_0ekoeag</outgoing></task><sequenceFlow id="Flow_05xtbpr" sourceRef="Gateway_10k824i" targetRef="Activity_17jbx0j" /><parallelGateway id="Gateway_10k824i"><incoming>Flow_0xv9yxo</incoming><outgoing>Flow_1wboruz</outgoing><outgoing>Flow_05xtbpr</outgoing></parallelGateway><sequenceFlow id="Flow_0ekoeag" sourceRef="Activity_17jbx0j" targetRef="Event_1hdhify" /></process><bpmndi:BPMNDiagram id="BpmnDiagram_1"><bpmndi:BPMNPlane id="BpmnPlane_1" bpmnElement="Process_1"><bpmndi:BPMNShape id="StartEvent_1y45yut_di" bpmnElement="StartEvent_1y45yut"><omgdc:Bounds x="152" y="102" width="36" height="36" /><bpmndi:BPMNLabel><omgdc:Bounds x="134" y="145" width="73" height="14" /></bpmndi:BPMNLabel></bpmndi:BPMNShape><bpmndi:BPMNShape id="Task_1hcentk_di" bpmnElement="Task_1hcentk"><omgdc:Bounds x="240" y="80" width="100" height="80" /></bpmndi:BPMNShape><bpmndi:BPMNShape id="ExclusiveGateway_15hu1pt_di" bpmnElement="ExclusiveGateway_15hu1pt" isMarkerVisible="true"><omgdc:Bounds x="395" y="95" width="50" height="50" /><bpmndi:BPMNLabel><omgdc:Bounds x="387" y="71" width="66" height="14" /></bpmndi:BPMNLabel></bpmndi:BPMNShape><bpmndi:BPMNShape id="Gateway_19khf0h_di" bpmnElement="Gateway_09q2xe7"><omgdc:Bounds x="395" y="215" width="50" height="50" /></bpmndi:BPMNShape><bpmndi:BPMNShape id="Activity_1yfhd3x_di" bpmnElement="Activity_1yfhd3x"><omgdc:Bounds x="690" y="200" width="100" height="80" /></bpmndi:BPMNShape><bpmndi:BPMNShape id="Event_1hdhify_di" bpmnElement="Event_1hdhify"><omgdc:Bounds x="1052" y="242" width="36" height="36" /></bpmndi:BPMNShape><bpmndi:BPMNShape id="Gateway_18yg547_di" bpmnElement="Gateway_10k824i"><omgdc:Bounds x="495" y="215" width="50" height="50" /></bpmndi:BPMNShape><bpmndi:BPMNShape id="Activity_17jbx0j_di" bpmnElement="Activity_17jbx0j"><omgdc:Bounds x="680" y="330" width="100" height="80" /></bpmndi:BPMNShape><bpmndi:BPMNEdge id="SequenceFlow_0h21x7r_di" bpmnElement="SequenceFlow_0h21x7r"><omgdi:waypoint x="188" y="120" /><omgdi:waypoint x="240" y="120" /></bpmndi:BPMNEdge><bpmndi:BPMNEdge id="SequenceFlow_0wnb4ke_di" bpmnElement="SequenceFlow_0wnb4ke"><omgdi:waypoint x="340" y="120" /><omgdi:waypoint x="395" y="120" /></bpmndi:BPMNEdge><bpmndi:BPMNEdge id="Flow_0xtm5qb_di" bpmnElement="Flow_0xtm5qb"><omgdi:waypoint x="420" y="215" /><omgdi:waypoint x="420" y="145" /></bpmndi:BPMNEdge><bpmndi:BPMNEdge id="Flow_0xv9yxo_di" bpmnElement="Flow_0xv9yxo"><omgdi:waypoint x="445" y="240" /><omgdi:waypoint x="495" y="240" /></bpmndi:BPMNEdge><bpmndi:BPMNEdge id="Flow_1wboruz_di" bpmnElement="Flow_1wboruz"><omgdi:waypoint x="545" y="240" /><omgdi:waypoint x="690" y="240" /></bpmndi:BPMNEdge><bpmndi:BPMNEdge id="Flow_1flrhu1_di" bpmnElement="Flow_1flrhu1"><omgdi:waypoint x="790" y="240" /><omgdi:waypoint x="921" y="240" /><omgdi:waypoint x="921" y="260" /><omgdi:waypoint x="1052" y="260" /></bpmndi:BPMNEdge><bpmndi:BPMNEdge id="Flow_05xtbpr_di" bpmnElement="Flow_05xtbpr"><omgdi:waypoint x="520" y="265" /><omgdi:waypoint x="520" y="370" /><omgdi:waypoint x="680" y="370" /></bpmndi:BPMNEdge><bpmndi:BPMNEdge id="Flow_0ekoeag_di" bpmnElement="Flow_0ekoeag"><omgdi:waypoint x="780" y="370" /><omgdi:waypoint x="916" y="370" /><omgdi:waypoint x="916" y="260" /><omgdi:waypoint x="1052" y="260" /></bpmndi:BPMNEdge></bpmndi:BPMNPlane></bpmndi:BPMNDiagram>
</definitions>
流程引擎架构
审批基本模型
审批表单:定制化表单,DIY审批内容
审批表单是一个简单且支持用户可配置的表单。因为现如今大多数 B 端产品都是以 SaaS 作为基础(如果是定制化产品,它的审批内容、流程也不会是固定不变的),这意味着审批表单需要为企业提供“DIY”的方式,通过表单提供不同的字段类型,去构建审批的实际要求。
通知渠道:通知审批过程、结果 消息渠道
通知渠道不隶属于审批流上下文,是审批流上下文中所对接的第三方系统。其作用是通知审批相关方审批结果并促使相关方快速做出判断及响应。通知渠道与企业工作沟通工具高度相关,包含但不限于:站内消息通知、短信通知、微信消息、钉钉消息等。
审批策略:自定义业务执行策略
上文可知,企业存在不同业务场景、特定的审批需求。在审批完成后,相应也存在不同的执行业务动作的策略。包括:自动执行,人工执行。
流程配置:自定义审批流程,选择参与方
- 串行审批流
- 并行审批流(或签 会签)
- 条件审批流
参与角色:
- 发起人
- 审批人
- 执行人
- 抄送人
Camunda流程引擎
表结构:
ACT_RE :'RE’表示 repository。 这个前缀的表包含了流程定义和流程静态资源 (图片,规则,等等)。
ACT_RU:'RU’表示 runtime。 这些运行时的表,包含流程实例,任务,变量,异步任务,等运行中的数据。 Flowable只在流程实例执行过程中保存这些数据, 在流程结束时就会删除这些记录。 这样运行时表可以一直很小速度很快。
ACT_HI:'HI’表示 history。 这些表包含历史数据,比如历史流程实例, 变量,任务等等。
ACT_GE: GE 表示 general。 通用数据, 用于不同场景下
ACT_ID: ’ID’表示identity(组织机构)。这些表包含标识的信息,如用户,用户组,等等。
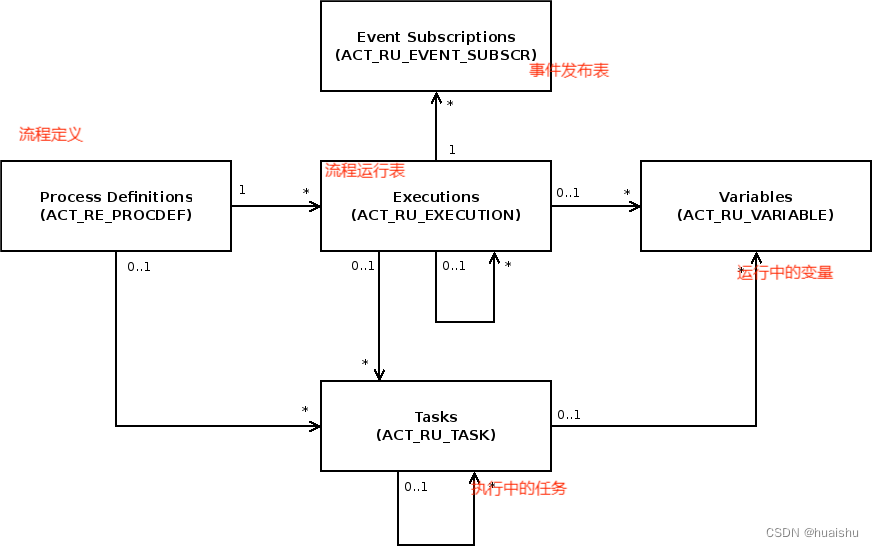
ACT_RE_PROCDEF 表包含所有已部署的流程定义。 它包括版本详细信息、资源名称或暂停状态等信息。
ACT_RU_EXECUTION 表包含所有当前执行。 它包括流程定义、父执行、业务密钥、当前活动以及有关执行状态的不同元数据等信息。
ACT_RU_TASK 表包含所有正在运行的流程实例的所有打开的任务。 它包括相应的流程实例、执行等信息以及创建时间、受让人或到期日期等元数据。
ACT_RU_EVENT_SUBSCR 表包含所有当前存在的事件订阅。 它包括预期事件的类型、名称和配置以及有关相应流程实例和执行的信息。
ACT_GE_SCHEMA_LOG 表包含数据库架构版本的历史记录。 当数据库模式发生更改时,新条目将写入表中。 创建数据库时会添加初始条目。
ACT_RU_METER_LOG 表包含运行时指标的集合,可以帮助得出有关 Camunda 平台的使用情况、负载和性能的结论。 指标以 Java 长范围内的数字形式报告,并对特定事件的发生进行计数。 请在指标用户指南中查找有关如何收集指标的详细信息。
ACT_RU_TASK_METER_LOG 表包含任务相关指标的集合,可以帮助得出有关 BPM 平台的使用情况、负载和性能的结论。
| 表分类 | 表名 |
| 一般数据 | |
| [ACT_GE_BYTEARRAY] | 通用的流程定义和流程资源 |
| [ACT_GE_PROPERTY] | 系统相关属性 |
| 流程历史记录 | |
| [ACT_HI_ACTINST] | 历史的流程实例 |
| [ACT_HI_ATTACHMENT] | 历史的流程附件 |
| [ACT_HI_COMMENT] | 历史的说明性信息 |
| [ACT_HI_DETAIL] | 历史的流程运行中的细节信息 |
| [ACT_HI_IDENTITYLINK] | 历史的流程运行过程中用户关系 |
| [ACT_HI_PROCINST] | 历史的流程实例 |
| [ACT_HI_TASKINST] | 历史的任务实例 |
| [ACT_HI_VARINST] | 历史的流程运行中的变量信息 |
| 流程定义表 | |
| [ACT_RE_DEPLOYMENT] | 部署单元信息 |
| [ACT_RE_MODEL] | 模型信息 |
| [ACT_RE_PROCDEF] | 已部署的流程定义 |
| 运行实例表 | |
| [ACT_RU_EVENT_SUBSCR] | 运行时事件 |
| [ACT_RU_EXECUTION] | 运行时流程执行实例 |
| [ACT_RU_IDENTITYLINK] | 运行时用户关系信息,存储任务节点与参与者的相关信息 |
| [ACT_RU_JOB] | 运行时作业 |
| [ACT_RU_TASK] | 运行时任务 |
| [ACT_RU_VARIABLE] | 运行时变量表 |
| 用户用户组表 | |
| [ACT_ID_BYTEARRAY] | 二进制数据表 |
| [ACT_ID_GROUP] | 用户组信息表 |
| [ACT_ID_INFO] | 用户信息详情表 |
| [ACT_ID_MEMBERSHIP] | 人与组关系表 |
| [ACT_ID_PRIV] | 权限表 |
| [ACT_ID_PRIV_MAPPING] | 用户或组权限关系表 |
| [ACT_ID_PROPERTY] | 属性表 |
| [ACT_ID_TOKEN] | 记录用户的token信息 |
| [ACT_ID_USER] | 用户表 |
业务流:
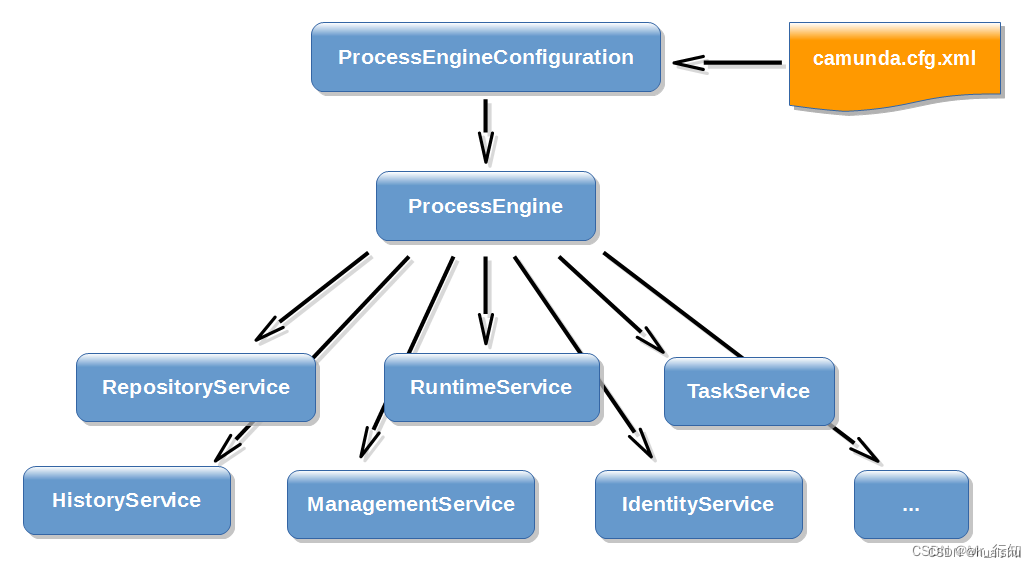
架构图:
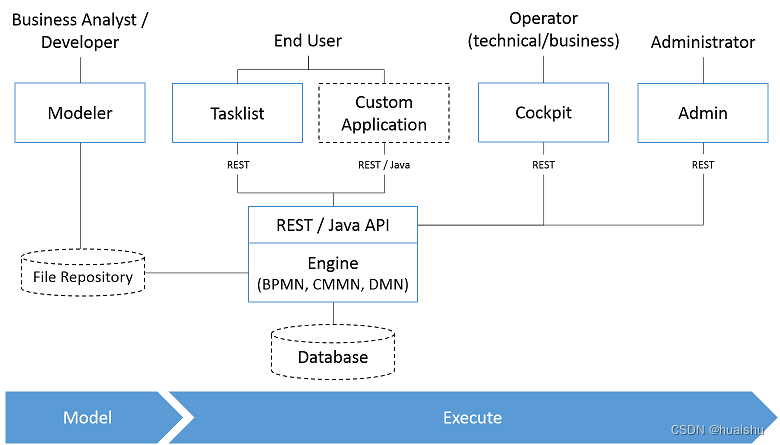
实战:
三条垂直线表示实例将并行执行,而三条水平线表示顺序【串行】执行。
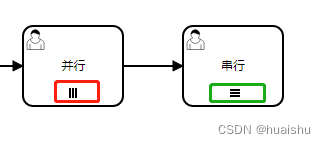
- nrOfInstances : 实例总数
- nrOfActiveInstances:当前活动的实例的数量。对于串行而言该值始终为1
- nrOfCompletedInstances:已经完成的实例数
- loopCounter 循环计数器
会签:${nrOfInstances == nrOfCompletedInstances} 表示所有人员审批完成后会签结束。
或签:${ nrOfCompletedInstances == 1}表示一个人完成审批,该会签就结束。
API接口:
参考:
BPMN这点事-BPMN的元素_bpmn元素-CSDN博客
BPMN 2.0详解 | Origin X Documentation
https://www.cnblogs.com/shizhe99/p/15321724.html
https://download.csdn.net/download/huaishu/88622081
BPMN Specification - Business Process Model and Notation
Camnuda 数据库 - ErBao's Docs
Camunda工作流多实例(会签/多人审批)_camunda 会签-CSDN博客
https://www.cnblogs.com/hezemin/p/17163018.html
