番禺人才网官方网站信息公布网站地图做计划任务
内存体系结构
目录
内存体系结构
2.1自动内存管理
2.2自动SGA内存管理
2.3手动SGA内存管理
2.3.1数据库缓冲区
2.3.1.1保留池
2.3.1.2回收池
2.3.2共享池
2.3.2.1SQL查询结果和函数查询结果
2.3.2.2库缓存
2.3.2.3数据字典缓存
2.3.3大池
2.3.4 JAVA池
2.3.5流池
2.4自动PGA内存管理
2.4.1查询内存使用情况
2.4.2设置最优的PGA工作区内存pga_aggregate_target
2.5手动PGA内存管理
数据库由磁盘文件构成,当数据库启动时,相关实例将被启动,而实例由内存结构和进程组成。数据库及其运行的程序存放在分配给内存的不同结构当中。我们只讨论单实例的内存体系结构。内存跟磁盘空间分配一样,一般情况下,我们只关注其大小,而内存的大小由各种
数据库内存参数控制。内存的大小可以手动分配,也可以自动分配,自动分配运行的更好,因此这里也只主要讨论自动分配的参数,记住这篇文章以专用服务器模式讲解,如果是共享服务器,并不适用
通过本章内容的学习,你将了解到:
- 为什么报错程序单元not found,清空共享池或者去掉全局变量即可解决
- 为什么同样一个查询,连续两次执行,第二次执行会比第一次执行快
- 如果函数执行的很慢,如何去优化
- 大型报表进行全表扫描,且里面有排序和聚合操作,导致速度特别慢,如何优化
- 为什么要使用绑定变量
- 内存结构分类
先熟悉几个名词
- SGA(System Global Area):系统全局区,一组共享内存结构,称为 SGA 组件,其中包含一个 Oracle 数据库实例的数据和控制信息。SGA 由所有服务器和后台进程共享
- PGA(Process Global Area):进程全局区,包含一个服务器进程的数据和控制信息的存储器区域。它是在服务器进程启动时由 Oracle 数据库创建的非共享内存
- UGA(User Global Area):用户全局区,是一个存储区(RAM),它保存的基于会话的信息。在专用服务器模式下运行时(一个会话 = 一个专用进程),UGA 存储在PGA(进程全局区域)中。
在共享服务器模式下运行时(具有共享服务器和调度程序的 MTS),会话可以由多个 服务器进程提供服务。因此,UGA 无法存储在PGA 中,而被移动到SGA(共享全局 区域)中。
- 内存管理
内存管理从上到下分别为
自动内存管理
手动内存管理->自动SGA内存管理
->手动SGA内存管理
->自动PGA内存管理
->手动PGA内存管理
内存管理分为自动和手动,自动内存管理是最顶层的内存管理,就是服务器动态分配SGA,PGA,UGA占用内存比例,只有禁用自动内存管理,才有可能启动自动或手动SGA,PGA内存管理

我们在2.3节会详细讲解上图中方框内的各个区域
2.1自动内存管理
自动内存管理,在操作系统可分配给数据库的内存中,设置参数MEMORY_TARGET,自动调整SGA和PGA的大小。
查看MEMORY_TARGET大小

当memory_target不等于0时,表示自动内存管理,等于0表示禁用自动内存管理
查看MEMORY_MAX_TARGET

Memory_max_target设置了memory_target最大可用大小。
memory_target是动态参数,可以通过alter system 语句执行修改,使用下列SQL查看是否是立即生效还是延迟生效

ISSES_MODIFIABLE:表示参数是否可以用ALTER SESSION( TRUE) 或不可以 ( FALSE) 改变
ISSYS_MODIFIABLE: 指示是否可以更改参数ALTER SYSTEM以及更改何时生效:
IMMEDIATE:无论用于启动实例的参数文件的类型如何,都可以使用ALTER SYSTEM更改参数。更改立即生效。
DEFERRED:无论用于启动实例的参数文件的类型如何,都可以使用ALTER SYSTEM更改参数。更改在后续会话中生效。
FALSE:除非使用服务器参数文件来启动实例,否则无法更改参数。更改在后续实例中生效。
启用自动内存管理将会自动分配,由下列参数控制的内存分配
DB_CACHE_SIZE
SHARED_POOL_SIZE
LARGE_POOL_SIZE
JAVA_POOL_SIZE
PGA_AGGREGATE_TARGET
Memory_target已经和Memory_max_target相等了,如果我们遇到了ORA-04031错误,这个错误原因是JAVA池大小不够,而JAVA池从SGA分配,如果我们采用自动内存管理,则需要扩大Memory_target,让数据库能分配更多内存给SGA,SGA再动态调整增加JAVA池大小,从而解决这个问题。所以要扩展Memory_target大小,必须首先扩充Memory_max_target大小,而Memory_target是不能使用alter system 语法进行修改,我们看下这个Memory_max_target是采用init.ora参数文件控制还是SPFILE服务器参数文件控制
init.ora 和 spfile 的区别。
- init.ora 和 spfile 都包含数据库参数信息。使用 spfile,您可以使用 ALTER SYSTEM 命令设置 Oracle 数据库设置,该命令在 sqlplus 中用于添加/修改/删除设置。但是对于 init.ora,您将其编辑为文本文件,因为 init.ora 以 ASCII 格式保存。
- init.ora 信息在数据库实例时被oracle 引擎读取。在 spfile 中的修改可以在不重新启动 oracle 数据库的情况下适用。
- 当 Oracle 数据库启动时,该进程将始终使用 spfile.ora(如果存在)。如果找不到 spfile.ora,则启动时将使用 init.ora。
Oracle 首先搜索 spfile[SID].ora 是否存在。如果没有,Oracle 将搜索 spfile.ora 参数文件。如果 spfile[SID].ora 和 spfile.ora 都不存在,Oracle 将使用 init[SID].ora 参数文件。
按照上面的思路,先查下spfile.ora是否存在

那么我们可以直接使用alter语句修改memory_max_target而不用去修改init.ora,后者还需要重启实例(虽然memory_max_target的ISSYS_MODIFIABLE=false,我们试试看看是否可行)
设置的数量不能大于操作系统最大可用内存,我们看下当前操作系统剩余内存

物理内存空闲的还有15m,虚拟内存4G,我们先扩展最大可用内存到1G
ALTER SYSTEM SET MEMORY_MAX_TARGET = 1024m SCOPE = SPFILE;
再次查询参数

看来还是要重启数据库
重启过程居然报错了
![]()
查了一下,设置一个1G超过了可用的最大内存。难道MEMORY_TARGET不能使用虚拟内存?
(我猜测可能的原因是,如果设置memory_max_target或memory_target超过了物理内存所允许的大小,数据库SGA或PGA将不得不占用虚拟内存,而数据库后台常驻的进程,一旦被页出到虚拟内存,再页入到物理内存中,其开销将是巨大的,因为常驻内存基本都是在运行,所以将会频繁的页入页出。但是大数据量排序的时候,超过了PGA排序区的内存,一定是从虚拟内存中拿的,这一部分超出的内存岂不是就超过了memory_target?)
使用free-h命令得出来可用内存是307m,那我先设置memoty_target为800m试试,现在因为数据库实例无法启动,无法继续执行ALTER SYSTEM SET MEMORY_MAX_TARGET语句,因此只能修改spfileORCL.ora文件,但是spfile是一个二进制文件,我们只能修改可读的文本文件,因此需要将二进制文件spfile导出成文本文件pfile,修改pfile之后,再导入回spfile
- 先备份文件
[root@MyHost ~]# cp /u01/dbs/spfileORCL.ora /u01/dbs/spfileORCL.ora.bak
然后创建文本文件
SQL> create pfile = '/u01/dbs/pfileORCL.ora' from spfile = '/u01/dbs/spfileORCL.ora';
- 修改文本文件
[root@MyHost ~]# vim /u01/dbs/pfileORCL.ora

改成800m之后按esc输入:wq保存退出
- 由文本文件pfile反向创建二进制文件spfile
SQL> create spfile='/u01/dbs/spfileORCL.ora' from pfile='/u01/dbs/pfileORCL.ora';
- 重启数据库
SQL> startup
查看memory_max_target

修改memory_target之前,我们先看下目前的实际内存占用
查看SGA内存占用

System Global Area就是SGA,差不多800m
或者使用下列SQL

查看PGA占用
SELECT round(SUM(pga_used_mem) / (1024 * 1024)
,2) MAX
,round(SUM(pga_alloc_mem) / (1024 * 1024)
,2) alloc
,round(SUM(pga_used_mem) / (1024 * 1024)
,2) used
,round(SUM(pga_freeable_mem) / (1024 * 1024)
,2) free
FROM v$process;
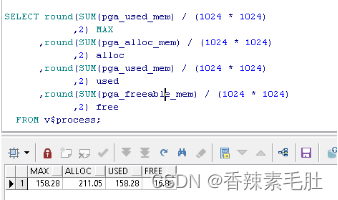
PGA占用158m.SGA占用800m
查看每一个会话占用内存情况
SELECT to_char(ssn.sid
,'9999') || ': ' ||
nvl(ssn.username
,nvl(bgp.name
,'background')) ||
nvl(lower(ssn.machine)
,ins.host_name) ssession
,to_char(prc.spid
,'999999999') pid_thread
,to_char((se1.value / 1024) / 1024
,'999g999g990d00') current_size_mb
,to_char((se2.value / 1024) / 1024
,'999g999g990d00') maximum_size_mb
FROM v$statname stat1
,v$statname stat2
,v$session ssn
,v$sesstat se1
,v$sesstat se2
,v$bgprocess bgp
,v$process prc
,v$instance ins
WHERE stat1.name = 'session pga memory'
AND stat2.name = 'session pga memory max'
AND se1.sid = ssn.sid
AND se2.sid = ssn.sid
AND se2.statistic# = stat2.statistic#
AND se1.statistic# = stat1.statistic#
AND ssn.paddr = bgp.paddr(+)
AND ssn.paddr = prc.addr(+);
现在我们修改memory_target大小
ALTER SYSTEM SET MEMORY_TARGET = 800m SCOPE = SPFILE;
Memory_target应该修改成多大,可以参考下面结果,当然越大越好,只不过多余的内存会用不到,造成浪费
SELECT m.*
,m.memory_size / m.memory_size_factor
FROM v$memory_target_advice m

当前大小是736,从第二行开始,当调整内存大于等于920m,则单位工作负载占用时间从1.0557降低到1,基本可以忽略不计,我的本地环境基本是零负载,所以降低为552也是可行
2.2自动SGA内存管理
SGA下有下列5个区域
- JAVA池
- 大池
- 共享池
- 流池
- 空池:包括固定SGA区,重做缓冲区,块缓冲区等
我们这里先不解释每个池和区都是干什么的,可以先看看他们的大小

从上到下分别是 共享池,java池,流池,空池,大池
再查查空池里面有什么

从上到下分别是固定区,块缓冲区,重做日志缓冲区,共享IO池
如果要启动自动SGA内存管理,首先需要关闭自动内存管理,然后开启自动SGA内存管理
11G之后,自动SGA内存管理ASMM已经被AMM取代了,这里不建议大家去修改,可以自己尝试
- 首先关闭自动内存管理
alter system set memory_target=0 scope=spfile;
(这里如果加了参数scope=spfile,需要重启数据库,要立即生效需要去掉scope=spfile,根据参数字段ISSYS_MODIFIABLE=IMMEDIATE判断是否能去掉)
- 修改sga_target和sga_max_size

在设置sga_target和sga_max_zise之后,系统会自动分配下列内存池的内存:
- 数据库缓冲区缓存(默认池) :参数DB_CACHE_SIZE
- 共享池:参数SHARED_POOL_SIZE
- 大池:LARGE_POOL_SIZE
- Java池:JAVA_POOL_SIZE
- 流池:STREAMS_POOL_SIZE
自动SGA内存管理不能分配,可能需要手动调整的:
- 重做日志缓冲区 (重做日志缓冲区的大小使用LOG_BUFFER初始化参数进行调整,如“配置重做日志缓冲区”中所述):参数LOG_BUFFER
- 其他缓冲区高速缓存(诸如KEEP,RECYCLE和其他非默认块大小)
在KEEP使用池的大小DB_KEEP_CACHE_SIZE初始化参数,如描述的那样,“配置KEEP池”。
在RECYCLE使用池的大小DB_RECYCLE_CACHE_SIZE初始化参数,如描述的那样,“配置循环池”。
- 固定 SGA 和其他内部分配
使用DB_nK_CACHE_SIZE初始化参数调整固定 SGA 和其他内部分配的大小。
使用下列SQL查询哪些SGA参数可以手动修改,比如采用自动SGA内存管理ASMM,虽然可以自动分配大池的大小,但是我们仍然可以手动修改
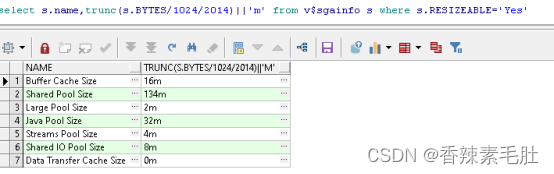
我们设置一下sga_target的值(对于专用服务器和共享服务器分别有一个分配原则,专用服务器建议50%作为SGA,共享服务器建议80%)
ALTER SYSTEM SET SGA_TARGET = 400M SCOPE = SPFILE;
Sga_max_size是初始化参数,需要关闭实例之后修改,因此我们就不去动了
查看SGA当前使用情况
SELECT m.component
,trunc(m.current_size / 1024 / 2024) || 'm' current_size
,trunc(m.min_size / 1024 / 2024) || 'm' min_size
,trunc(m.max_size / 1024 / 2024) || 'm' max_size
FROM v$memory_dynamic_components m

- 修改STATISTICS_LEVEL为TYPICAL或者ALL

默认就是typical所以不用修改
最后重启一下数据库(虽然参数ISSYS_MODIFIABLE是immediate,我修改后查询memory_target还是736m

原因是我的修改语句是alter system set memory_target=0 scope=spfile;
后面这个scope=spfile应该去掉,加上这个参数表示修改参数文件spifle,而不是修改系统参数并立即生效
)
查看参数

这样就成功启用了ASMM自动SGA内存管理
2.3手动SGA内存管理
只需要将sga_target修改成0,即可启用手动SGA内存管理
alter system set sga_target=0 scope=spfile;(后面的scope=spfile可以去掉,不然要重启数据库,alter system用法
Alter system set xxx=xxx scope= memory|spfile|both
memory表示修改内存,当前生效,重启后失效
Spfile静态参数必须使用该关键词,重启后生效
Both表示默认值
)
手动SGA内存管理,可以手动修改下列参数
- DB_CACHE_SIZE 块缓冲区
- SHARED_POOL_SIZE 共享池
- LARGE_POOL_SIZE 大池
- JAVA_POOL_SIZE JAVA池
- STREAMS_POOL_SIZE 流池
- INMEMORY_SIZE 内存池
前5个参数刚好是自动SGA内存管理自动调整的参数,第6个是内存池,详细参考
In-Memory Column Store Architecture
通俗来说,数据库缓冲区以行模式缓存,内存列以列模式缓存
下面主要讲解块缓冲区和共享池调优,这两个是SGA最重要的部分
更多数据库内存层面性能调优请参考https://docs.oracle.com/database/121/TGDBA/memory.htm#TGDBA508
2.3.1数据库缓冲区
数据库缓冲区也叫数据库高速缓存(也有叫块缓冲区,对应参数db_cache_size),当执行SQL时,数据从磁盘读取,放到内存中,之后SQL执行结束后,这段内存区域并不会被清空或覆盖,而是作为一个缓存,下一个SQL查询数据时,会优先从数据库缓冲区去拿数据,拿不到再经过磁盘IO获取数据。整个系统运行过程中,从数据库缓冲区拿数据越多,则说明内存命中率越高。
这个缓冲区必须位于SGA,因为PGA的共享程度并没有SGA高
查看数据库缓冲区大小

结果居然是0,这个0肯定不对,那么我们可以查询v$sgastats表,查看所有SGA具体情况

Buffer_cache就是快缓冲区大小(这里显示48m是因为我后面执行完脚本再截的图,快缓冲区主要由默认池+保留池+空池组成)
数据库缓冲区主要有三个池构成
- 默认池
Default pool 执行SQL后,从磁盘拿到的数据库,默认放在这个池中
- 保留池
Keep pool 池的大小是固定的,因此不会缓存所有的块,当采用LRU原则,最不常用的块会被老化退出,那些频繁访问的块,将会放在保留池中,以免被挤出缓冲区
- 回收池
Recycle pool 当某些块访问次数不频繁,比如每月才执行的一次报表,或者select *from table 全表扫描,拿到的数据就会放在保留池中,这些数据会很容易被老化退出。跟其它高级语言的内存回收机制有点像,引用计数,用一次,计数器+1,每隔一段时间,找那些计数器值最小的,将其从内存中释放。
我们查一下这三个池的大小

红框中从上到下分别是默认池,保留池,回收池
然后执行下列SQL
DECLARE
l_rec dba_objects%ROWTYPE;
CURSOR a_cur IS
SELECT * FROM dba_objects d;
BEGIN
FOR a_rec IN a_cur
LOOP
l_rec := a_rec;
END LOOP;
END;
再次查询
SELECT component
,current_size / 1024 / 1024 || 'm' current_size
,max_size / 1024 / 1024 || 'm' max_size
,min_size / 1024 / 1024 || 'm' min_size
FROM v$sga_dynamic_components s;

默认池数据增大到了48m,因为上面的代码,读取数据将会缓存到块缓冲区(数据库缓冲区,这两者是一个意思,所以我经常会混用)中
既然数据会从块缓冲区中读取,那么我修改了数据并提交了,磁盘的块数据和内存块的数据不就不一致了吗?原因是执行一次update,发生了下面这些事情
在SGA生成回滚段(undo),然后修改SGA块缓冲区的值,然后对前面的操作生成重做日志(redo),然后使用进程DBWn将这些数据发生更新的块,写入磁盘中,最后使用进程LGWR将日志缓冲区内容写入磁盘。所以从顺序上讲,一定是先更新内存,再更新磁盘,这样就能保证数据从块缓冲区读取,一定是修改后的数据。我们把数据发生更新的块叫做“脏块”,当这些“脏块”对应的数据被写入磁盘之后,磁盘数据和块缓冲区数据一致了,这些“脏块”就变成了“干净块”。当发生数据修改时,不会马上把“脏块”的数据写入磁盘,因为这些数据块还可能再次发生修改,写磁盘是一个很慢的操作,当遇到:没有任何可用缓冲区(没有“干净块”),“脏块”过多,三秒超时,监测点这四种情况才会发生DMWn写入。
我们现在已经知道了块缓冲区的作用,且内存调参,也就是调整这些内存的大小,那么多大的块缓冲区最合适,是不是越大越好呢?
缓冲区大小和IO消耗的关系如下

来源:Tuning the Database Buffer Cache
纵坐标是IO造成的读取瓶颈,横坐标是数据库缓冲区大小,A增加到B,和B增加到C,增大了相同的缓存,性能的提升前者大一点,按下面的操作,看看合适的数据库缓冲区大小是多大
查看数据库缓冲区建议助手DB_CACHE_ADVICE是否开启

然后查看优化建议视图
SELECT size_for_estimate
,buffers_for_estimate
,estd_physical_read_factor
,estd_physical_reads
FROM v$db_cache_advice
WHERE NAME = 'DEFAULT'
AND block_size =
(SELECT VALUE FROM v$parameter WHERE NAME = 'db_block_size')
AND advice_status = 'ON';
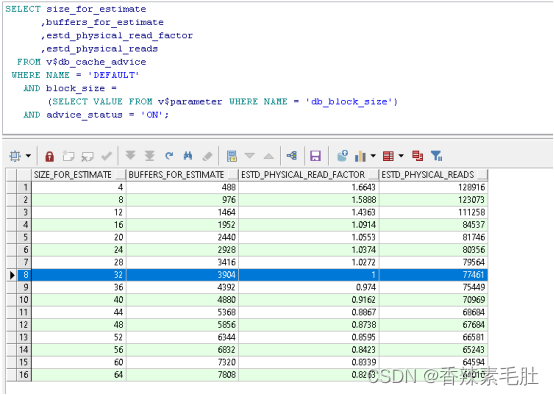
可以看到当前块缓冲区大小是32m,当增加到36m时,物理读将会从77461减少到75449,磁盘IO读取“可能”会减小至0.974。
我们计算一下,增加单位块缓冲区大小,对性能的影响

我的测试环境,块缓冲区大小增加到44m,单位性能提升最大,再往下逐次递减,所以宝贵的内存空间还是不要全放在这里了。(如果DB_CACHE_SIZE设置的过大,超过了实际可用的物理内存,将会使用SWAP交换分区,速度将会非常慢,这个问题一般不会出现,但是如果出现了,需要知道这个知识点)
另一个更直观的指标是最开始提到的数据缓存命中率。想要的数据都在内存中,对应的命中率越高。执行下列SQL查看数据库缓存命中率
SELECT NAME
,VALUE
FROM v$sysstat
WHERE NAME IN ('db block gets from cache'
,'consistent gets from cache'
,'physical reads cache');
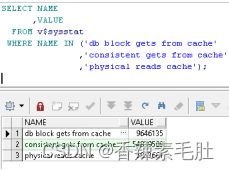
计算公式是1 - (('physical reads cache') / ('consistent gets from cache' +
'db block gets from cache'))
通过上面的公式得出来当前命中率为0.90922536184953。命中率需要高于95%,所以当前设置的DBA_CACHE_SIZE一定是偏小的。
上面的命中率是块缓冲区的命中率,块缓冲区有三个池构成,我的测试环境只配置了默认池,单独查默认池的命中率SQL如下
SELECT NAME
,physical_reads
,db_block_gets
,consistent_gets
,1 - (physical_reads / (db_block_gets + consistent_gets)) "Hit Ratio"
FROM v$buffer_pool_statistics
WHERE NAME = 'DEFAULT'
需要注意的是,命中率是一个动态的东西,可能现在是90%,当执行那些不常用的报表操作时,命中率可能会降低到50%以下,较低的命中率意味着较高的IO,而IO的速度比内存慢千倍。最好能统计出每分钟的命中率变化情况,以及当较低命中率出现的时候,当前系统的状态,同时运行了哪些程序,这个工作AWR或STATSPARK已经完成了,需要对照AWR报告进行调优,参考价值更大。
现在我们手动修改一下db_cache_size
首先需要确认是否关闭了自动内存管理和自动SGA内存管理(按照步骤来做的话一定是都关闭的)

然后修改db_cache_size,修改之前查询一下参数属性,看到immediate表示可以修改

alter system set db_cache_size=1m;

说明修改的1M没有效果,小于4m的数字会自动设置为4m;
然后执行下列查询
select * from dba_objects d where d.OBJECT_NAME like 'CUX%'
按前面给出的步骤,再次查询命中率,降低到了0.86.
(没有合适的测试环境,这样调优属于盲人摸象,没办法直观的看出来调优的效果,因为我的数据库负载太低了)
命中率是越高越好吗?
请看ORACLE官方的解释
低缓存命中率并不一定意味着增加缓冲区缓存的大小将有利于性能。此外,高缓存命中率可能错误地表明缓冲区缓存的大小适合工作负载。
要解释缓冲区缓存命中率,请考虑以下因素:
通过一次性处理或优化SQL语句,避免重复扫描频繁访问的数据。
重复扫描同一个大表或索引会人为地增加低缓存命中率。检查频繁执行的具有大量缓冲区获取的SQL 语句,以确保这些SQL 语句的执行计划是最优的。
通过在客户端程序或中间层缓存经常访问的数据,避免重新查询相同的数据。
在运行 OLTP 应用程序的大型数据库中,许多行仅访问一次(或从不访问)。因此,在使用后将块保留在内存中是没有意义的。
不要连续增加缓冲区缓存大小。
如果数据库正在执行全表扫描或不使用缓冲区高速缓存的操作,则缓冲区高速缓存大小的持续增加不会产生任何影响。
当发生大型全表扫描时,请考虑低命中率。
在长时间的全表扫描期间访问的数据库块放置在最近最少使用 (LRU) 列表的尾端,而不是列表的头部。因此,在执行索引查找或小表扫描时,块比读取的块老化得更快。
查询某个表的块缓存情况
- 先执行查询
SELECT COUNT(1) FROM CUX_TEST3
Cux_test3是我建立的一个表,1000000行左右,这个表只有一个字段,每一行存入的都是字符”A”
- 然后查询获取object_id
SELECT data_object_id
,object_type
FROM dba_objects
WHERE object_name = upper('CUX_TEST3');
得到的data_object_id=101739
- 然后查询缓存情况
SELECT COUNT(*) buffers FROM v$bh WHERE objd = 101739;
结果是461个块,上面的count(*)查询,且没有索引,因此一定是全表扫描
- 查询块缓冲区的情况
SELECT name, block_size, SUM(buffers)
FROM V$BUFFER_POOL
GROUP BY name, block_size
HAVING SUM(buffers) > 0;
Sum求和的结果是488
- 计算命中率
461/488=0.94
2.3.1.1保留池
前面说到数据库缓冲区(数据库高速缓存或块缓冲区)有三个小区域,默认池,保留池,回收池。一般情况下,只启用默认池,我们2.3.1主要是在默认池下的操作。对于保留池,指的是你期望留在内存中,而不会随着访问频率降低,自动老化退出的表或块。
KEEP 池是小表、全表扫描的绝佳存储位置。它也可以是存储来自经常使用的段中的数据块的好地方,这些段消耗了数据缓冲区中的大量块空间。这些块通常位于通过索引访问的小型引用表中,并且不会出现在全表扫描报告中。
当一个表不得不进行频繁全表扫描,那么这个表最好是一直放在内存中,但是假如这个表很大(但是又不能过大),将把默认池的其它缓存对象挤出,为了防止这种情况,可以把表缓存到保留池。同理,一周或一个月执行一次的报表系统,这种不频繁的全表扫描应该把表放在回收池(或者禁用内存缓存,因为超大的表只要放到内存中,一定会挤出其它正在用的缓存对象)
- 哪些对象需要放在保留池里
ORACLE告诉我们:
“将段放入 KEEP 池的一个很好的候选者是一个小于 DEFAULT 缓冲池大小 10% 并且已经产生至少 1% 的系统中总 I/O 的段。”。
我的初始默认池是48m,那么执行全表扫描的小表的大小应该是小于4m的表。怎么查询表大小呢?当然是查询表段的大小

13m有点太大了。且这个表段还要由于频繁全表扫描影响性能,所以CUX_TEST3表不适合放入保留池,下面我只是演示一下如何放入保留池
- 先修改保留池的大小
alter system set db_keep_cache_size=20m scope=both;
修改完毕我们查询一下
成功修改为20m
我们清空一下块缓冲区
alter system flush buffer_cache;
然后执行全表扫描的时间差不多是0.05秒,当放入保留池之后,保留池只有这一个对象,也不会老化退出,因此执行时间都会很快
- 将表缓存放入保留池中
alter TABLE apps.cux_test3 storage (buffer_pool keep);
- 查询保留池中有哪些对象

- 还原为默认池
alter TABLE apps.cux_test3 storage (buffer_pool DEFAULT);

2.3.1.2回收池
回收池操作跟保留池一样,能使用到这两个池的场景非常少见,因此大家知道有这个东西就行了。更多内容参考
Oracle RECYCLE Pool
2.3.2共享池
数据库缓冲区和共享池是SGA中最重要的两个区域,通过前面的内容我们了解到数据库缓冲区是用于缓存数据,减少磁盘IO,而共享池用于缓存程序和SQL。
共享池由三个组件组成(类比数据库缓冲区也有三个部分)
- 数据字典缓存
- SQL查询结果和函数查询结果
- 库缓存
因为共享池如此重要,我在这里会给出两个示例,详细描述一下。
2.3.2.1SQL查询结果和函数查询结果
首先准备测试表和测试数据
1.创建测试表
create table cux_number_test(a number) tablespace APPS_DATA_TABLESPACE nologging;
2.填充数据
insert /*+ append */ into cux_number_test (a)
select trunc(dbms_random.value(1, 1000000000))
from dual
connect by level <= 100000000;
填充过程报错了,很显然内存爆了,上面的语句我们使用了connect by 语句,会占用PGA的sort_area_size排序区,这个报错我们先放着,后面讲到PGA的时候我们再来解决这个问题

我们将connect by 改成循环,1亿数据量我估算一下,差不多要写入800m数据,等了半个小时,才写入300m,不等了,先改成100万试试
DECLARE
BEGIN
FOR i IN 1 .. 1000000
LOOP
INSERT /*+ append */
INTO cux_number_test
(a)
VALUES
(trunc(dbms_random.value(1
,1000000000)));
END LOOP;
COMMIT;
END;
最后我共写入了300万数据,
然后创建一个耗时特别长的函数,比如最简单的求质数的函数(图省事可以直接使用DBMS_LOCK.SLEEP,因为使用缓存的结果是不真正执行函数)
CREATE OR REPLACE PACKAGE cux_test_pkg IS
FUNCTION is_prime_number(p_number IN NUMBER) RETURN VARCHAR2;
END cux_test_pkg;
CREATE OR REPLACE PACKAGE BODY cux_test_pkg IS
FUNCTION is_prime_number(p_number IN NUMBER) RETURN VARCHAR2 IS
BEGIN
--小数和负数不是质数
IF p_number <> trunc(abs(p_number))
THEN
RETURN 'N';
END IF;
IF p_number = 1
THEN
RETURN 'N';
ELSIF p_number IN (2
,3)
THEN
RETURN 'Y';
ELSE
FOR i IN 2 .. p_number - 1
LOOP
IF MOD(p_number
,i) = 0
THEN
RETURN 'N';
END IF;
END LOOP;
RETURN 'Y';
END IF;
RETURN 'N';
END is_prime_number;
END cux_test_pkg;
然后执行下列SQL
SELECT COUNT(*)
FROM cux_number_test
WHERE cux_test_pkg.is_prime_number(a) = 'Y'
当ORACLE优化器拿到这个SQL,首先分析得出来cux_number_test是一个表,select count from where = 这些都是关键词,cux_test_pkg.is_prime_number是一个函数,那么判断哪些是关键词,哪些是视图还是表,哪些是函数,使用数据字典去判断,比如拿到cux_number_test,就执行查询select object_type from dba_objects where object_name=’cux_number_test’(举个例子);每次都需要执行查询,才知道这个字符串对应的对象是什么,那么为了省去解析的时间,将数据字典名称-对象结果缓存到数据字典缓存组件中。上面的SQL最佳的执行计划是什么,优化器分析出来没有建立索引,也没有创建函数索引,最佳方式是全表扫描, 因此把生成的执行计划缓存到库缓存中。cux_test_pkg.is_prime_number是一个函数,函数作为PLSQL代码,会从数据字典对应的磁盘中取出来,将最终的可执行代码放入库缓存缓存起来。同时cux_test_pkg.is_prime_number(a)的结果,
以及整个SQL查询的结果,也会放入共享池的SQL查询结果和函数查询结果缓存中。
总结一下,共享池缓存了数据字典,缓存了执行计划,缓存了PLSQL代码,缓存了函数结果集和SQL结果集。共享池会自动判断表数据是否发生了变化,当数据发生变化了,那么缓存结果就一直有效。
现在看看我们的查询结果,我等了半个小时,都没查询出来。
我们可以估算一下,执行8位数质数的操作大概是2秒,三百万行数据就是600万秒,那基本是查不出来结果了。
我们单独分析下面一个SQL
SELECT cux_test_pkg.is_prime_number(59184740) FROM DUAL;
第一次执行的时候是2秒,你再次重复执行,结果变成了0.035秒。过一会再次执行,时间又变成了2秒,你反复不停的执行,发现最后时间一直稳定在0.02秒上下。
怎么解释这种情况呢?
第一次执行,数据库需要分析语义,查询每个字符串到底对应什么数据库对象过程中会生成数据字典缓存,然后生成执行计划到库缓存中,读取函数,生成可执行的文件,放入库缓存,然后开始执行查询并返回数据。59184740是一个偶数,所以mod(59184740,2)就得出来不是质数,计算的结果只需要0.01秒,前面的这一系列操作需要花费2秒。
所以重复执行的过程中,一直就是最后的0.01秒。
过一会执行,这些共享池的缓存的东西,被老化退出了,因此需要重复执行
反复不停的执行,这些缓存的东西被加热的过热,就不容易被老化退出,所以一直是这个结果。
我们再看下面这个SQL
SELECT cux_test_pkg.is_prime_number(10000103) FROM DUAL;
这个SQL固定需要7秒,因为这个数是一个大质数,所以他会一直循环10000102接近1千万次。前面说到,共享池不是会自动缓存函数和SQL查询结果,为什么没有缓存下来呢?
查看是否开启缓存结果集

0表示未开启
查看所有result_cache参数

result_cache_mode:可以通过三种方式启用结果缓存:通过提示、更改会话或更改系统。默认为 MANUAL,这意味着我们需要通过 RESULT_CACHE 提示显式请求缓存;使用FORCE 就不需要显示指定请求缓存,例如ALTER SESSION SET result_cache_mode = FORCE
- result_cache_max_size:这是结果缓存的大小(以字节为单位)。缓存直接从共享池中分配,但单独维护(例如刷新共享池不会刷新结果缓存);
- result_cache_max_result:指定单个结果集能够使用的最高缓存百分比(默认为 5%);和
- result_cache_remote_expiration:这指定基于远程对象的结果集可以保持有效的分钟数。默认值为 0,这意味着不会缓存依赖于远程对象的结果集。
先看看共享池是否为非0

然后查看参数修改方式

执行修改
alter system set result_cache_max_size=20m scope=both;
both表示同时修改当前设置的参数立即生效,以及spfile参数文件永久生效
查询result_cache_max_size仍然是0,重启一下数据库
仍然是0,执行下列查询
SELECT dbms_result_cache.status FROM dual;
表示未开启结果集缓存
看来这个both参数并不能修改静态参数。
执行下列语句
alter system set result_cache_max_size=20m scope=spfile;
然后重启服务器
查看结果


再次执行sql

时间从7秒瞬间降低到0.045秒
11g检查是否开启结果集缓存参考
query result cache in oracle 11g
我们看看执行计划

可以看到执行计划使用了结果集缓存,我们查询一下
SELECT id
,TYPE
,creation_timestamp
,block_count
,column_count
,pin_count
,row_count
FROM v$result_cache_objects
WHERE cache_id = '9fkm9w7qgbx441pz3a7xbkncxt';

占据了一个块大小
我们可以估算一下,三百万数据的函数结果集,全部缓存到内存中,大概需要5m数据。
全表扫描然后缓存到内存可行,但是全表执行函数的时间是不可预计的。因此我们用部分行数据测试,我们先为a列建立索引,然后就能选出一百行数据进行测试
create index cux_number_test_n1 on cux_number_test(a)tablespace APPS_IDX_TABLESPACE;
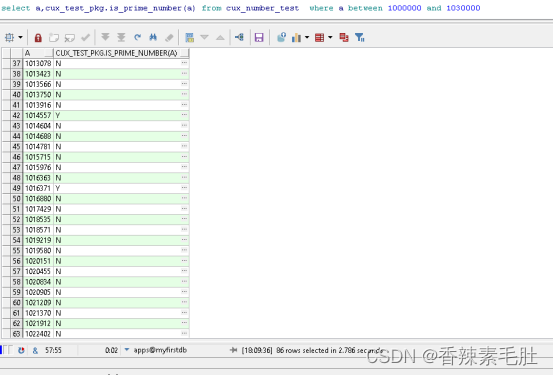
重复执行仍然需要2.78秒,我们进行结果集缓存
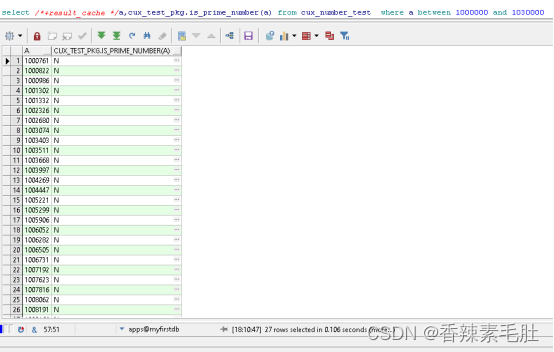
第一次执行仍然需要2-3秒,第二次之后,速度降低到0.1秒。
现在我们执行一下子查询,看是否会缓存子查询结果

仍然有效。
我们更换一下SQL语句,对比一下执行计划


仅仅是数据范围不一样,结果执行计划使用的缓存集并不一样,也就是第二行sql执行时间仍然要7秒。而并没有复用100000到103000之间的结果集。
我们更改为绑定变量的形试,SQL文本是一样的情况,是否会复用结果集
DECLARE
i NUMBER := 1000000;
j NUMBER := 1030000;
k NUMBER;
BEGIN
SELECT /*+result_cache */
COUNT(1)
INTO k
FROM cux_number_test
WHERE a BETWEEN i AND j
AND cux_test_pkg.is_prime_number(a) = 'Y';
END;
DECLARE
i NUMBER := 1000000;
j NUMBER := 1030000-1;
k NUMBER;
BEGIN
SELECT /*+result_cache */
COUNT(1)
INTO k
FROM cux_number_test
WHERE a BETWEEN i AND j
AND cux_test_pkg.is_prime_number(a) = 'Y';
END;
第二个脚本在第一个脚本执行之后,仍然需要3秒时间,未复用结果集。同样我采用临时表的方式,往临时表写入数据,保证执行前后的SQL一模一样,仍然未复用。因此这个结果集缓存,只能用于一模一样的SQL,同时所用的表数据还不能发生变化,且不存在标量子查询才可用。
( select ( select /*+result_cache */ cux_test_pkg.is_prime_number(10000103) from dual) from dual;
这就是一个标量子查询,永远无法用到结果集缓存
下面这个可以
select * from ( select /*+result_cache */ cux_test_pkg.is_prime_number(10000103) from dual)
)
仅仅上面这个例子,可以考虑建议函数索引,物化视图,或者直接把计算的结果,永久保存下来,然后建立10000103:Y这样的关系,比如建立一个对照表,比结果集缓存效果更好。所以各位有新特性一定要搞清楚局限性,再去使用。
查看官方给出的哪些无法缓存的情形:
在 SQL 查询中使用以下数据库对象或函数时,无法缓存结果:
- 字典和临时表
- 序列CURRVAL和NEXTVAL伪列
- SQL 函数current_date、current_timestamp、local_timestamp、userenv/sys_context(带有非常量变量)sys_guid、sysdate、 和sys_timestamp
- 非确定性 PL/SQL 函数
如果查询中使用了以下任何构造,则缓存结果将使用参数值进行参数化:
- 绑定变量。
- 以下 SQL 函数:dbtimezone、sessiontimezone、userenv/sys_context(带有常量变量)uid、 和user。
- NLS 参数。
那么就没有办法了吗?答案是在函数包中增加result_cache。我们试试函数包中添加result_cache,看看效果
包头和包体添加下列关键词


SQL结果集使用条件太苛刻了,必须是最终执行的SQL文本一模一样(大小写不同不影响最终执行的SQL),因此我们试试,在不同情况下的函数结果集缓存
为了演示方便,我把cux_number_test写入连续的100万大数
truncate table cux_number_test;
begin
for i in 10000000..11000000 loop
insert into cux_number_test(a) values(i);
end loop;
commit;
end;
- 执行脚本(有效)
DECLARE
i NUMBER := 1000000;
j NUMBER := 1030000 ;
k NUMBER;
BEGIN
SELECT COUNT(1)
INTO k
FROM cux_number_test
WHERE a BETWEEN i AND j
AND cux_test_pkg.is_prime_number(a) = 'Y';
END;
修改不同的 i,j ,比如将j减小100,速度仍然很明显,将j增加100,可能增加100次函数执行,原有的数据不影响,最终时间仍然是0.04s
- 标量子查询(有效)-
select * from ( select cux_test_pkg.is_prime_number(10000103) from dual) ;
select ( select cux_test_pkg.is_prime_number(10000103)from dual )from dual ;
- 临时表子查询(有效)
create global temporary table cux_test_tmp(a number) ON COMMIT PRESERVE ROWS tablespace APPS_TMP_TABLESPACE
insert into cux_test_tmp(a)values(10000121)
SELECT *
FROM cux_number_test ct
WHERE EXISTS (SELECT 1 FROM cux_test_tmp t WHERE ct.a = t.a)
AND cux_test_pkg.is_prime_number(ct.a) = 'Y';
- 函数带有SYSDATE(有效,但返回错误的值)
在我们cux_test_pkg.is_prime_number添加sysdate

执行第一条SQL,在使用第二条的时候,仍然会使用缓存
select cux_test_pkg.is_prime_number(a) FROM cux_test_tmp where a in(10000121,10000103)
select cux_test_pkg.is_prime_number(a) FROM cux_number_test where a in(10000121,10000103)
- 函数使用sysdate(无效)

上面的写法每隔一秒,所以返回值应该从null和Y不停变换
执行下面的SQL
能使用缓存,但是执行结果确实一直是NULL,说明数据是缓存下来了,但是结果是错误的
因此这个“确定性”非常重要。
函数本身需要是确定的,出参严格由入参决定,注释掉result_cache就可以了。
所有随机函数和上下文变量也不用测试了。
我们最后做一个测试,根据表数据动态发生变化,函数结果集缓存是否有效
- 函数返回结果跟表数据有关(部分有效,总是返回正确结果)

insert into cux_test_tmp(a)values(1);
select cux_test_pkg.is_prime_number(10000121) from dual;
测试结果,能返回正确的结果,但是只要当前会话cux_test_tmp上的事务不提交,则缓存一直失效,只有commit之后,数据才有结果。
我们将临时表更换为正式版试试,有效
测试结果:
- 执行函数的会话,不能含有当该函数含有表的事务,如果有且未提交,则缓存不起用,每次会重新计算
- 另一个会话,含有事务,缓存起作用。将事务提交,重新执行函数而不重新计算
7.函数语句内使用SYSDATE(有效,但返回错误数据)

create table cux_test4(s date ,e date);
insert into cux_test4(s,e)values(sysdate ,sysdate+1/24/3600*10)
select cux_test_pkg.is_prime_number(10000121) from dual
写入的数据,10秒后就会失效,但是执行函数返回结果,一直是Y
想要返回正确的结果,只能修改函数为cux_test_pkg.is_prime_number(p_number,p_date),将trunc(sysdate)作为参数传入。
函数结果集和SQL结果集,既然都是缓存在内存中,同样有内存命中率的问题,统计内存命中率更多内容请参考http://www.oracle-developer.net/display.php?id=503
使用alter system flush shared_pool刷新共享池并不会清空结果集缓存,因为他们在共享池的不同区域,刷新共享池只是清空了库缓存,也就是执行计划和可执行plsql函数文件
要想清空结果集缓存请使用
BEGIN
dbms_result_cache.flush;
END;
关闭结果集缓存请使用(传入false表示开启)
BEGIN
dbms_result_cache.bypass(TRUE);
END;
关于dbms_result_cache的用法参考https://docs.oracle.com/database/121/ARPLS/d_result_cache.htm#ARPLS67656
使用select * from V$RESULT_CACHE_OBJECTS;查询缓存对象
执行了前两句之后,查询结果如下

注:11g测试发现要想使用函数结果集缓存,则函数内部需要写result_cache关键字
,且sql中也需要/*+ result_cache*/ hint
2.3.2.2库缓存
我们经常会遇到一个词叫“硬解析”,解决硬解析的方式是使用绑定变量,否则会造成
- 系统花费大量的CPU资源解析SQL语句
- 使用大量的资源管理共享池中不被重用的对象
- 闩等待
但是绑定变量只有在动态SQL中出现,我们的代码很少出现绑定变量,为什么并没有明显感受到性能下降
请看下面三个SQL
SELECT COUNT(*) FROM cux_number_test;
SELECT COUNT(*) FROM CUX_NUMBER_TEST;
SELECT COUNT(*) /*123 */ FROM CUX_NUMBER_TEST;
他们的SQL文本不一样,但是并不需要额外为第2,3行创建执行计划



三张图的 Plan Hash Value : 3499252087
查询一下具体的执行计划

Plan hash value一样,执行计划就一样
所以即使我们执行的SQL文本不一样,ORACLE内部也会尝试解析成一模一样的sql可执行文本。我们通过sql_id查询一下

那么下面这两个SQL是一样的SQL吗
SELECT COUNT(*) FROM cux_number_test WHERE a = 1;
SELECT COUNT(*) FROM cux_number_test WHERE a = 2;

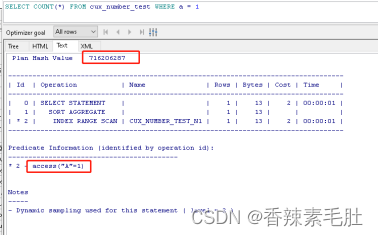
PLAN HASH VALUE仍然一致,就算从a=1执行到a=100000他们执行计划相同,不会造成共享池的库缓存爆满。
ORACLE的机制导致了,不会要求sql语句只有发生了改变,就会重新生成执行计划。所以“硬解析”更多的是其它客户端访问ORACLE数据库时发生,比如JDBC
我们使用下面一段代码访问我们的数据库
package org.example;
import java.sql.*;
import oracle.jdbc.*;
import oracle.jdbc.pool.OracleDataSource;public class TestSqlPlanLoop {public static void main(String[] args) throws SQLException {OracleDataSource ods = new OracleDataSource();ods.setURL("jdbc:oracle:thin:apps/apps@myhost:1521:ORCL");//建立连接Connection conn = ods.getConnection();//创建语句Statement stmt = conn.createStatement();ResultSet rset;//运行查询,返回结果集对象for (int i = 10000000; i <= 10002000; i++) {rset = stmt.executeQuery("SELECT /*test*/ a FROM apps.cux_number_test WHERE a =" + i);// while (rset.next()) {// System.out.println(rset.getString(1));// }}//rset.close();//关闭结果集对象stmt.close();conn.close();}
}上面代码就是循环执行了select a from cux_number_test where a=……两千次
(如果你并行执行上面的代码,你就可以直观看到闩等待带来的影响了,因为他们会争用数据字典的解析)
(如果需要在你的IDEA执行,需要安装JDBC驱动,可以参考https://blog.csdn.net/xiaojinlai123/article/details/79447727)
那么如何去看硬解析次数,库缓存性能,答案是使用statspack或者AWR查看。上次文档已经告诉大家如何安装,这个我们执行完之后,将生成的statspack文件打开,这个文件目录在
$ORACLE_HOME/rdbms/admin下,以lst后缀结尾,比如我的长这样

我们只关注硬解析部分以及库缓存相关指标(文件中还有数据库缓冲区 buffer cache 监控指标,buffer get越高,命中率也越高(所以命中率高并不代表性能好),但是磁盘IO也很高,表示有大量全表扫描。磁盘IO低的话,表示扫描了大量无效索引)

硬解析次数每秒29.4次

库缓存命中率66.04%,而正常的值应该是95%以上的
最后看看Pct Misses指标

这三个值需要低于1%才合理。
我们将上面的JDBC代码改成绑定变量再试试(只是演示硬解析用,如果要取2000个数据不需要执行两千次SQL)
package org.example;
import oracle.jdbc.pool.OracleDataSource;
import java.sql.*;
public class TestSqlPlanLoopBind {public static void main (String[] args ) throws SQLException{OracleDataSource ods = new OracleDataSource();ods.setURL("jdbc:oracle:thin:apps/apps@myhost:1521:ORCL");//建立连接Connection conn = ods.getConnection();//创建语句String sql = "SELECT /*test*/ a FROM apps.cux_number_test WHERE a =?";ResultSet rset;PreparedStatement stmt = conn.prepareStatement(sql);for (int i = 10000000; i <= 10002000; i++) {stmt.setInt(1, i);rset = stmt.executeQuery();// while (rset.next()) {// System.out.println(rset.getString(1));// }}stmt.close();conn.close();}
}执行上面的JAVA代码前后,执行 statspack.snap拿到快照id,然后获取快照文件

硬解析从每秒29降低到6

库缓存命中率从66.04%提升到84.93%(低于95%都是有问题的)

Pct miss降低了20%,但是仍然还是这么高,肯定还是有别的问题,我们有机会再去查这个问题。
使用下列SQL查询当前会话游标缓存命中率
SELECT cach.value cache_hits
,prs.value all_parses
,round((cach.value / prs.value) * 100
,2) AS "% found in cache"
,cach.sid
FROM v$sesstat cach
,v$sesstat prs
,v$statname nm1
,v$statname nm2
WHERE cach.statistic# = nm1.statistic#
AND nm1.name = 'session cursor cache hits'
AND prs.statistic# = nm2.statistic#
AND nm2.name = 'parse count (total)'
AND prs.value <> 0
AND cach.sid = &sid
AND prs.sid = cach.sid;
查看库缓存命中率
SELECT namespace
,pins
,pinhits
,reloads
,invalidations
,pinhits / pins
FROM v$librarycache
where pins<>0
ORDER BY namespace;

即使我们采用了绑定变量,库缓存命中率仍然这么低,考虑是不是共享池太小导致的
因此开始我们的共享池调优,之后再对比库缓存命中率
- 查看共享池大小

- 查看共享池空闲大小
SELECT bytes / 1024 / 1024 || 'm'
FROM v$sgastat
WHERE NAME = 'free memory'
AND pool = 'shared pool';

共享池只要有剩余就行,且共享池不宜过大
- 查看共享池内存顾问
首先看参数是否是typical或all

然后查询共享内存顾问视图
SELECT shared_pool_size_for_estimate
-- 估计的共享池大小(以兆字节为单位)
,shared_pool_size_factor
-- 与当前共享池大小相关的大小因子
,estd_lc_size
-- 库缓存使用的估计内存(以兆字节为单位)
,estd_lc_memory_objects
-- 指定大小的共享池中库缓存内存对象的估计数量
,estd_lc_time_saved
-- 由于在指定大小的共享池中找到了库缓存内存对象,因此估计已保存的解析时间(以秒为单位)。这是在共享池中重新加载所需对象(如果它们因可用空闲内存量不足而过期)所花费的时间。
,estd_lc_time_saved_factor
-- 与当前共享池大小相关的估计解析时间节省因子
,estd_lc_load_time
-- 在指定大小的共享池中解析所用的估计时间(以秒为单位)
,estd_lc_load_time_factor
-- 相对于当前共享池大小的估计加载时间因子
,estd_lc_memory_object_hits
-- 在指定大小的共享池中找到库缓存内存对象的估计次数
FROM v$shared_pool_advice
结果如下

可以看到,共享池内存从204增加240,显著减小了加载时间因子。
- 查看库缓存重载次数
select * from V$LIBRARYCACHE

其中reload次数应该接近0最优,命中因子应该接近1
- 修改shared_pool_size

alter system set shared_pool_size=240m ;
- 测试
再次执行带绑定变量的JDBC程序,查看STATSPACK报告
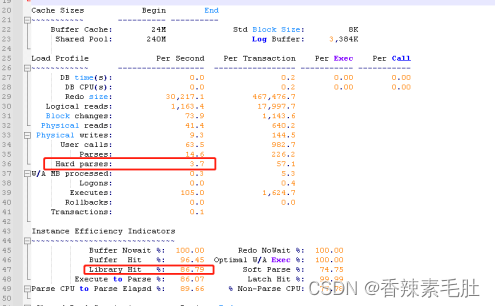
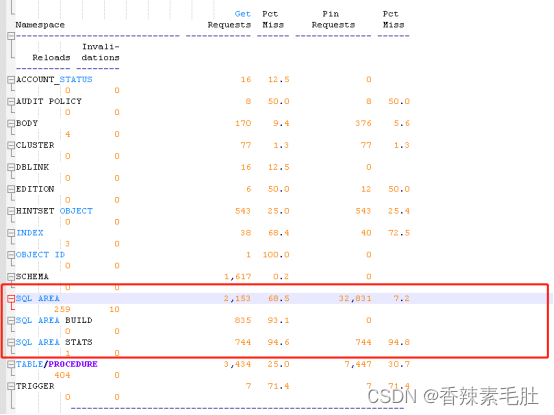
效果不是很明显,略微提升了一点点。也可能是statspack报告没有那么精确,我执行的时间段在10秒内,需要20分钟-1小时的统计数据,误差会小点
除了执行计划缓存在库缓存中,执行的PLSQL代码也缓存在其中,如果某些包的代码行数很多,(比如超过1万行),最好的方式是固定在库缓冲区中,防止reload.因为正常情况包不是整段加载而是分段加载的,前面加载的代码段很可能被老化退出。
查看哪些包需要“固定”
SELECT owner, name, type, sharable_mem, loads, kept, executions, locks, pins
FROM v$db_object_cache outer
WHERE type in ('PROCEDURE','PACKAGE BODY', 'PACKAGE', 'FUNCTION', 'TRIGGER', 'SEQUENCE')
AND kept = 'NO'
and executions > ( select 2*avg(count(executions))
FROM v$db_object_cache inner
WHERE type in ('PROCEDURE','PACKAGE BODY', 'PACKAGE', 'FUNCTION', 'TRIGGER', 'SEQUENCE')
AND kept = 'NO'
group by executions)
and loads > ( select 2*avg(count(loads))
FROM v$db_object_cache inner
WHERE type in ('PROCEDURE','PACKAGE BODY', 'PACKAGE', 'FUNCTION', 'TRIGGER', 'SEQUENCE')
AND kept = 'NO'
group by loads)
ORDER BY executions DESC;
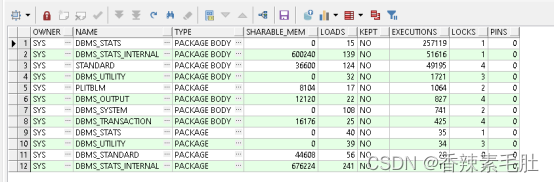
我们将DBMS_STATS_INTERNAL包缓存进内存(需要管理员账号)
begin
dbms_shared_pool.keep('SYS.DBMS_STATS_INTERNAL','P');
end;
2.3.2.3数据字典缓存
数据字典缓存也称为“行缓存”。用于储存最近使用的对象定义。比如
Select * from dba_objects, dba_objects是一个视图,而不是一个基表等等。
数据字典缓存对象定义,加快语句分析速度,而不需要真正查询数据字典表。
那么,我们经常会看见开发规范里面,需要添加ower,也是段的拥有者,比如上面应该改写成select * from sys.dba_objects,能显著减少减少字典缓存中的条目数。为一个对象建立的同义词越多,越需要添加段拥有者。
2.3.3大池
大池中的“大”字,并不是大容量的内存,而是大块内存,共享池的内存是按块分配的,大段内存的分配需要使用大池。我们只需要在下面的情况下才考虑使用大池。注意大池不存在老化退出的机制
- 共享服务器
在共享服务器架构中,每个客户端进程的会话内存都包含在共享池中。查询连接模式

所有会话都是专用模式,因此不需要考虑
- 并行查询
并行查询使用共享池内存来缓存并行执行消息缓冲区。
- 恢复管理器
恢复管理器 (RMAN) 使用共享池在备份和还原操作期间缓存 I/O 缓冲区。对于 I/O 服务器进程、备份和恢复操作,Oracle 数据库分配大小为几百 KB 的缓冲区
2.3.4 JAVA池
Java 池内存在服务器内存中用于 JVM 中所有特定于会话的 Java 代码和数据。Java 池内存的使用方式不同,具体取决于 Oracle 服务器运行的模式。
Java Pool Advisor 统计信息提供有关用于 Java 的库缓存内存的信息,并预测 Java 池大小的变化如何影响解析率。当statistics_level设置为TYPICAL或更高时,Java Pool Advisor 在内部打开。当顾问关闭时,这些统计信息会重置。
注意,JAVA代码不在JAVA池中缓存,而是跟PLSQL包一样,在共享池的库缓存中
2.3.5流池
在单个数据库中,您可以指定从 SGA 中称为 Streams 池的池中分配 Streams 内存。要配置流池,请使用STREAMS_POOL_SIZE初始化参数以字节为单位指定池的大小。如果未定义 Streams 池,则在第一次使用 Streams 时会自动创建一个。
如果SGA_TARGET设置,则Streams池的SGA内存来自SGA的全局池。如果SGA_TARGET未设置,则 Streams 池的 SGA 将从缓冲区缓存中传输。此传输仅在首次使用 Streams 后发生。转移的金额是共享池大小的 10%。
2.4自动PGA内存管理
PGA是操作系统某个进程或线程专用的内存,我们执行SQL语句,其中的排序和散列连接,都是在PGA完成的,详细如下:
- 基于排序的运算符,如ORDER BY,GROUP BY,ROLLUP,和窗口函数
- 哈希连接
- 位图合并
- 位图创建
- 写入批量加载操作使用的缓冲区
设置自动PGA内存管理步骤如下:
- 确认workarea_size_policy是否为AUTO

- 确认pga_aggregate_target参数为非0值

这个参数只是设置的PGA上限,而且也不是硬性规定,除非使用参数PGA_AGGREGATE_LIMIT
过多的 PGA 使用会导致高交换率。发生这种情况时,系统可能会变得无响应和不稳定,所以才需要这个参数。
Oracle 建议最初将 20% 的可用内存专用于 PGA,80% 专用于 SGA。因此,OLTP 系统的参数初始值PGA_AGGREGATE_TARGET可以计算为:总共物理内存*0.8*0.2
我的物理内存是2g,因此PGA大概是320M
表示启动了PGA内存管理
2.4.1查询内存使用情况
1.查看当前系统PGA使用情况
select p.name ,p.value/1024/1024||'m' value from V$PGASTAT p;

设置的PGA内存是536M,实际分配296M,实际使用192m可以释放85M

命中率一栏可以看到为100%,一趟排序就能完成
查看具体某个进程的PGA内存情况
SELECT s.sid
,s.program
,p.pga_alloc_mem / 1024 / 1024 --已分配内存
,p.pga_used_mem / 1024 / 1024 --已用内存
,p.pga_freeable_mem / 1024 / 1024 --可释放内存
FROM v$session s
,v$process p
WHERE s.paddr = p.addr
ORDER BY p.pga_used_mem DESC
当然对v$process表求和就能得到所有的PGA内存

结果和v$pgastat一致

2查看历史记录中多道排序的次数
SELECT low_optimal_size / 1024 / 1024 low_mb
,(high_optimal_size + 1) / 1024 / 1024 high_mb
,optimal_executions
,onepass_executions
,multipasses_executions
FROM v$sql_workarea_histogram
WHERE total_executions != 0;

multipasses_executions表示多趟排序的执行次数,前面的两列表示占用的内存范围
3查看当前会话的内存使用情况
SELECT sql_hash_value --正在执行SQL的哈希值
,sql_id --正在执行SQL的标识符
,sql_exec_start --执行开始时间
,workarea_address --工作区主键
,operation_type --操作类型
,policy --工作区调整策略
,sid --会话id
,active_time --处于活动状态的平均时间
,work_area_size / 1024 / 1024 work_area_size --工作区大小
,expected_size / 1024 / 1024 expected_size --期望大小
,actual_mem_used / 1024 / 1024 actual_mem_used --实际内存使用
,max_mem_used / 1024 / 1024 max_mem_used --最大内存使用
,number_passes
,tempseg_size / 1024 / 1024 tempseg_size --分配内存不足以至于占用临时表空间大小
,tablespace --表空间名称
FROM v$sql_workarea_active
因为我当前没有执行排序和hash连接,所以上面查询结果为空,执行两个sql给大家演示一下

查询表v$sql_workarea_active结果如下

SID刚好是467,操作是sort,使用内存13m,tempseg_size为空,表示排序未占用磁盘临时段进行排序
通过SQL_ID可以查表

就能知道占用内存的SQL语句是哪个。
表v$sql_workarea_active不会记录所有的SQL执行情况,只有那些占用内存较多的会话才会被记录在这张表里,且只会查询当前的内存情况,历史情况需要查询表v$sql_workarea
再来演示一个hash_join的操作,一般没有索引的小表连接就会采用这张方式,当然我们也可以是手动指定hash_join
SELECT */*+use_hash(d1,d2) */
FROM cux_number_test d1
,cux_number_test d2
WHERE to_char(d1.a)||'1' = to_char(d2.a)||'1'
因为这个a字段有索引,因此只能采用这张方式强制使索引失效,然后把数据放到内存里,进行hash连接
然后查询表v$sql_workarea_active结果如下

操作类型是hash-join,使用内存62m
- 查询单道和多道排序次数
SELECT NAME profile
,cnt
,decode(total
,0
,0
,round(cnt * 100 / total)) percentage
FROM (SELECT NAME
,VALUE cnt
,(SUM(VALUE) over()) total
FROM v$sysstat
WHERE NAME LIKE 'workarea exec%');
2.4.2设置最优的PGA工作区内存pga_aggregate_target
SELECT p.pga_target_for_estimate / 1024 / 1024
,p.*
FROM v$pga_target_advice p
查询结果如下

可以看到 当前PGA内存是536M,实际设置402M时,pga命中率就达到100%,因此缩小PGA内存,给更多的内存空间给共享池和块缓冲区
alter system set pga_aggregate_target=300m
直接设置PGA排序和散列参数为300M,等系统运行一段时间之后,再次查询该PGA顾问视图,看看命中率情况,然后继续调参……直到最佳的PGA内存大小,良好的SQL查询不需要很大的PGA内存,应该把内存分配给块缓冲区,然后是库缓存
2.5手动PGA内存管理
尽管 Oracle 数据库支持手动 PGA 内存管理,但 Oracle 强烈建议改用自动内存管理或自动 PGA 内存管理。
所以这一节内容只是做演示,意义不大。没有谁会使用手动PGA内存管理。当然特殊情况除外。查看PGA有关内存参数

可以看到前三个参数是可以在会话级别修改的,因此我们可以模拟出这样的场景,排序或散列操作超过了PGA可用内存,导致磁盘IO,通过增加内存区域减少IO。
sort_area_size:排序占用的内存大小
sort_area_retained_size:排序完毕之后保留的内存大小,为0表示不保留
hash_area_size:哈希连接占用的内存大小
执行下列SQL
SELECT *
FROM (SELECT d1.*
,rownum row_number
FROM dba_dependencies d1
,dba_dependencies d2
WHERE d1.referenced_name = d2.name
AND d1.referenced_type = d2.type
AND d1.referenced_owner = d2.owner
ORDER BY 1 DESC)
WHERE row_number BETWEEN 728000 AND 729600
居然出现了临时表不足的报错
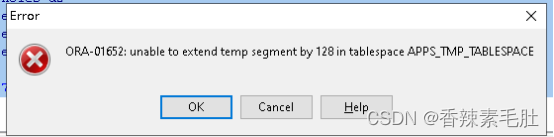
说明排序或者散列区不够用了,需要从临时段里拿空间。我们等会再来解决这个临时表空间不足的问题,按照我们之前的思路,给当前会话启用手动PGA内存管理,然后给PGA排序或散列区扩容,就能保证不出现这个问题。
- 首先查询一下到底需要多少内存
我们使用v$sql_workarea_active表拿不到这个数据,因此只能显示正在运行的内存情况,因此我们记录下当前SQL对应的SQL_ID,去历史表查询

将查询结果传入下面的SQL_ID中,得到总共内存使用情况
SELECT s.last_memory_used / 1024 / 1024 last_memory_used
,s.last_tempseg_size / 1024 / 1024 last_tempseg_size
,s.max_tempseg_size / 1024 / 1024 max_tempseg_size
,s.multipasses_executions
,(s.last_memory_used + s.max_tempseg_size) / 1024 / 1024 total
FROM v$sql_workarea s
WHERE s.sql_id = '35q8aqsb1dwvf'
ORDER BY 5 DESC

可以看出来总共使用了42M内存,这42M是包括了散列和排序的,没办法区分到底排序用了多少,散列用了多少(散列用于哈希多表连接),而且因为我的排序区不够,导致最终SQL执行失败了,所以最终使用内存可能超过50m.我们直接将排序和散列区都设置为100M(实际上我们需要扩充临时段,才能知道最终SQL执行完毕需要多少内存,我第一次设置50m仍然报错临时段不足)
- 设置当前会话参数
alter session set workarea_size_policy=manual;--设置当前会话PGA参数手动管理
alter session set hash_area_size=104857600;--散列区100m
alter session set sort_area_size=104857600;--排序区100m
alter session set sort_area_retained_size=0;--保留区0m,表示排序完毕释放排序区内存
- 同一会话中执行查询
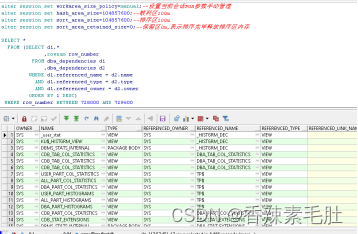
未出现临时表空间不足错误
- 查询内存使用情况

看到居然是排序占用了90m物理内存,88m临时表空间的IO,但是有点奇怪,这个TABLESPACE不是不能自动扩展吗?
- 设置表空间自动扩展,修复表空间不足BUG
当然也可以创建数据文件

APPS_TMP_TABLESPACE表空间差不多还剩1m可用

报错提示无法扩展128个块,刚好就是1m
先改成自动扩展
alter database tempfile '/usr/local/oracle19c/oradata/ORCL/APPS_TMP_TABLESPACE.dbf' autoextend on
然后新开一个窗口,执行查询,然后查询内存情况

然后看看我们临时表空间扩容了多少

扩容了345m
到这里ORACLE内存结构差不多讲完了,最后我们恢复我们的自动内存管理
- 设置MEMORY_TARGET和MEMORY_MAX_TARGET
ALTER SYSTEM SET MEMORY_TARGET = 800m SCOPE = SPFILE;
2.重启数据库
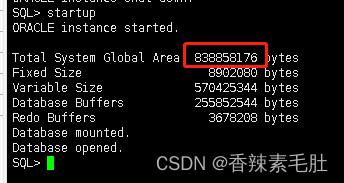
这个838858176字节刚好就是800m,表示成功启用了自动内存管理
========================================
作者正在找工作,有推荐的工作机会请联系我
========================================
