网站开发技术是什么免费自助建站哪家好
InteIIiJ IDEA 2023.2版本发布了,在2023.2中,官方根据用户的宝贵反馈对新UI做出了大量改进,新UI界面大大减少了干扰,可以让用户更好地专注于代码。相信很多同学都已经迫不及待地尝试了。

安装激活好 Intellij idea 之后,再搭配如下的插件,工作效率将提升十倍。
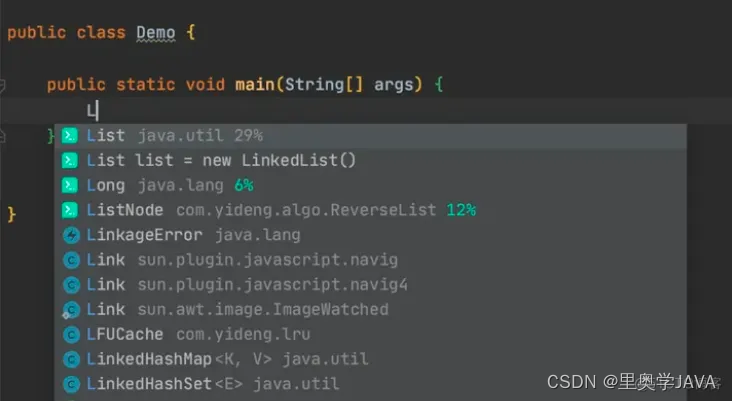
1. Codota 代码智能提示插件
只要打出首字母就能联想出一整条语句,这也太智能了,还显示了每条语句使用频率。
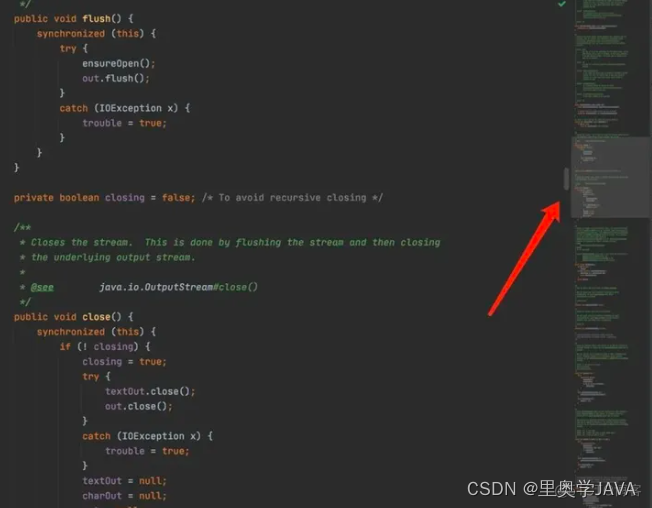
2. CodeGlance 显示代码缩略图插件
当代码很多的时候,方便查看,很有用。
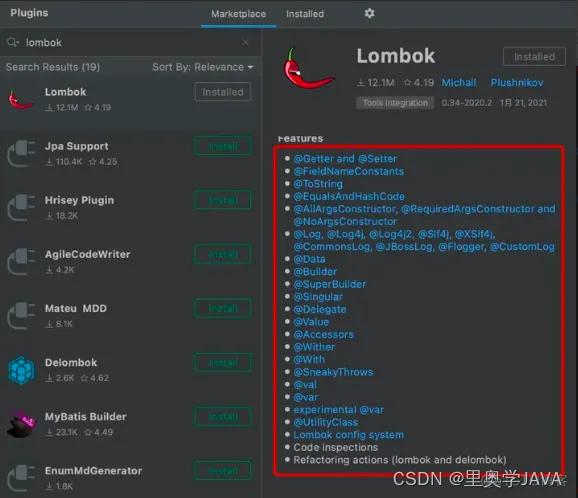
3. Lombok 简化臃肿代码插件
实体类中的get/set/构造/toString/hashCode等方法,都不需要我们再手动写了
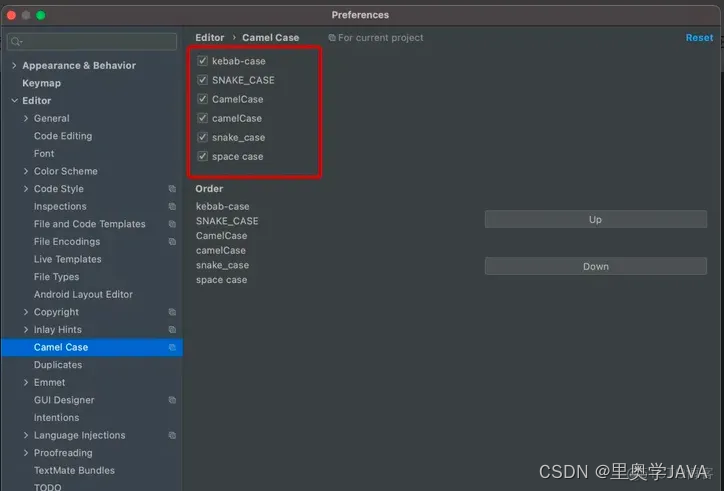
4. CamelCase 驼峰命名和下划线命名转换
这几种风格的命名方式,用快捷键 ⇧ + ⌥ + U / Shift + Alt + U可以进行快速转换,当我们需要修改大量变量名称的时候很方便。
5.MybatisX 高效操作Mybatis插件
一款基于 IDEA 的快速开发插件,方便在使用mybatis以及mybatis-plus时简化繁琐的重复操作,提高开发速率。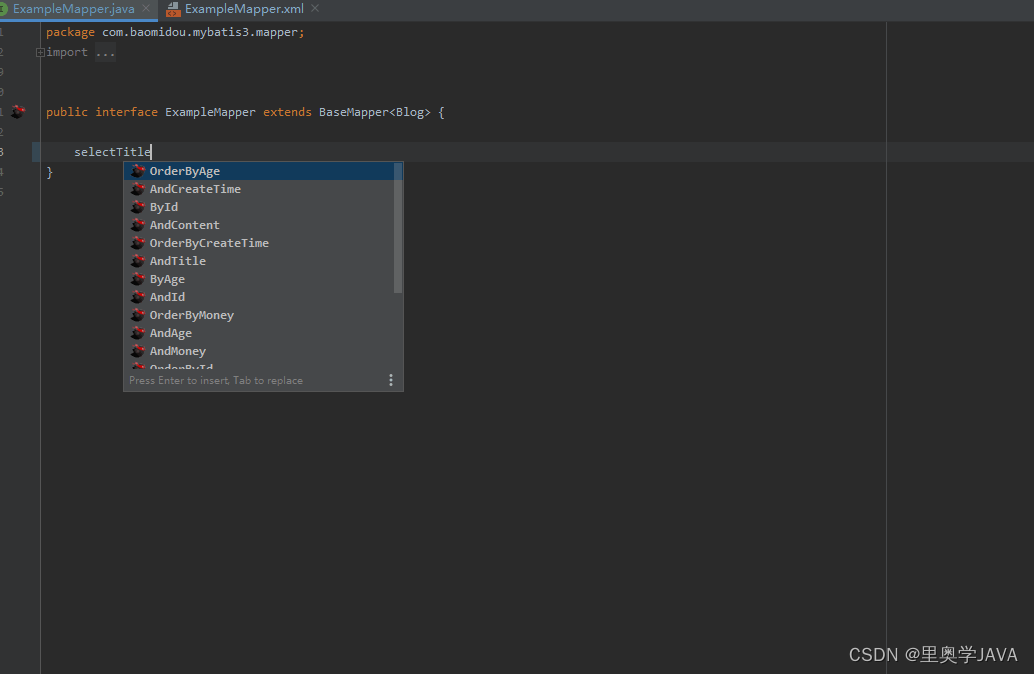
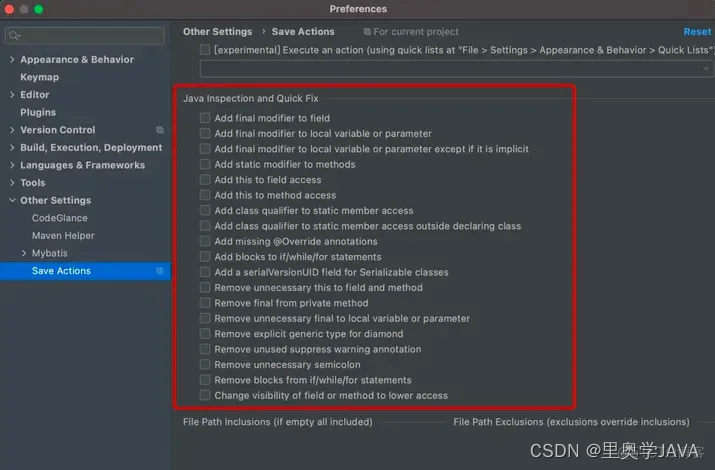
6. Save Actions 格式化代码插件
可以帮忙我们优化包导入,自动给没有修改的变量添加final修饰符,调用方法的时候自动添加this关键字等,使我们的代码更规范统一。
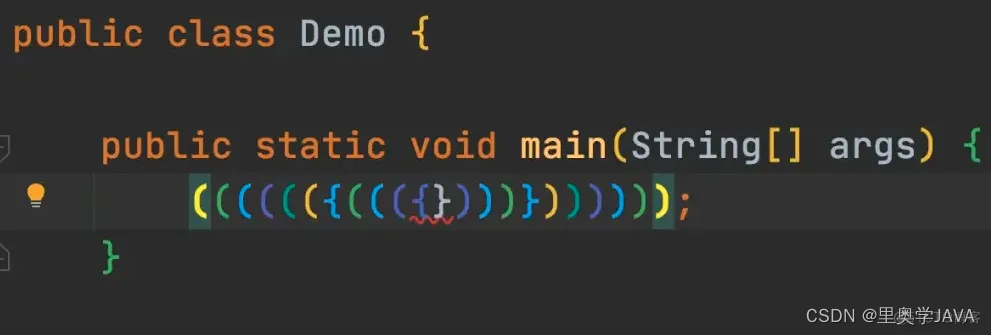
7. Rainbow Brackets 彩虹括号插件
成对儿的括号显示相同的颜色,有了这个插件,我的近视都好了。